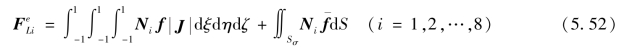5.4 8结点六面体三维实体等参单元
当结构不能简化为平面问题时,需要划分为三维实体单元进行分析。典型的三维实体单元为六面体单元,六面体单元可以取为8个角结点,称为8结点三维实体元。如果在六面体的每条棱边中点各增加一个结点(称为边中结点),每个单元就有20个结点,这种单元称为20结点三维实体单元。
图5.9(b)为一个任意8结点六面体单元,与平面问题类似,建立一个与此单元对应的边长为2的8结点正立方体单元,并建立局部坐标系ξηζ,坐标原点在正立方体的形心,如图5.6(a)所示,此即母单元。
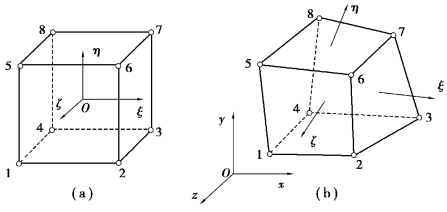
图5.9 8结点六面体单元
(1)母单元位移函数
参照式(4.41),母单元的位移模式设为
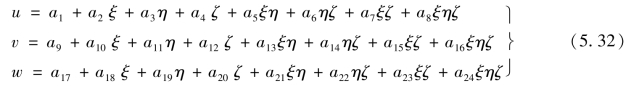
单元插值函数可以表示为
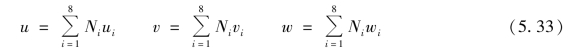
式中Ni(ξ,η)为形函数,参照式(4.52)由式(5.34)给出
![]()
式中,ξ0=ξiξ,η0=ηiη,ζ0=ζiζ。
式(5.33)可写作矩阵形式
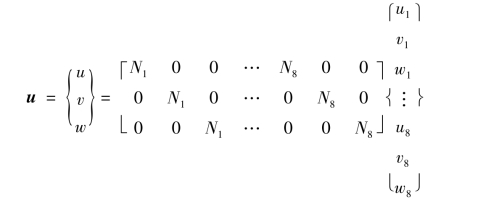
即
![]()
(2)等参坐标变换
对图5.6(b)所示为整体坐标系xyz与图5.6(a)所示局部坐标系ξηζ两种坐标系采用式(5.36)进行变换
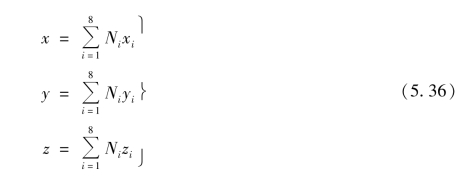
式中,变换函数Ni(ξ,η)即为位移函数(5.20)中的形函数。
坐标变换式(5.36)使实际的任意8结点六面体子单元[图5.6(a)]与8结点正立面体母单元[图5.6(b)]的8个角结点一一对应,子单元6个平面、12条直边与母单元6个平面、12条直边一一对应,并使子单元内各点与母单元各点一一对应。这样相当于把实际的任意六面体子单元映射为正立方体母单元。
(3)单元刚度矩阵
将式(5.33)代入几何方程,可得单元应变列阵

则式(5.35)可以写为
![]()
其中,B——单元几何矩阵。
参照2.2.5节分析,根据最小势能原理可得到单元刚度矩阵计算公式,即

式中,D为三维弹性矩阵:
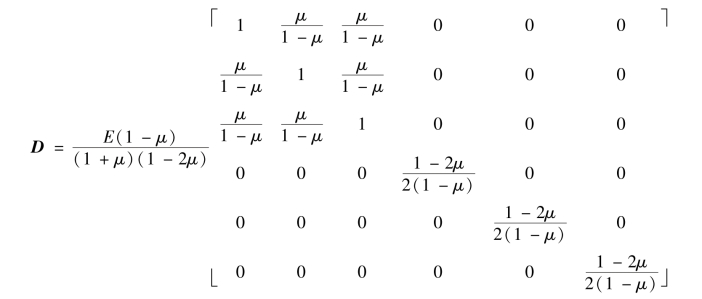
由式(5.38)可以看到,矩阵B中的元素是形函数对整体坐标x,y,z的偏导数,而形函数是局部坐标ξ,η,ζ的函数,所以,要计算形函数Ni对x,y,z的导数,需要进行坐标变换。
与平面等参单元单元刚度矩阵的计算方法类似,根据复合函数求导规则,由坐标变式(5.36),有
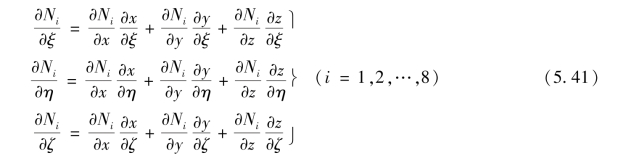
或用矩阵表示为
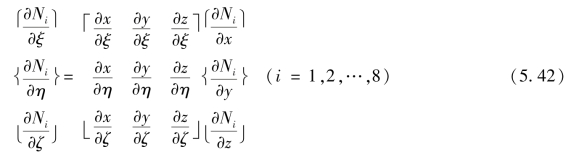
即
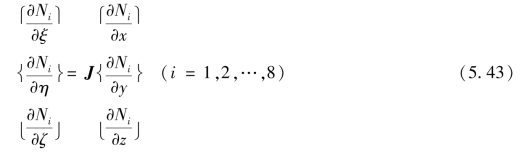 (https://www.daowen.com)
(https://www.daowen.com)
式中,J为坐标变换的雅可比矩阵
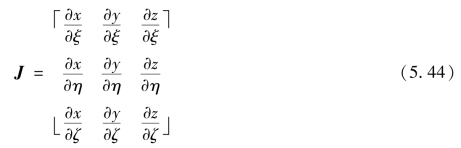
对式(5.29)两边左乘以雅可比矩阵的逆矩阵J-1,则可得到
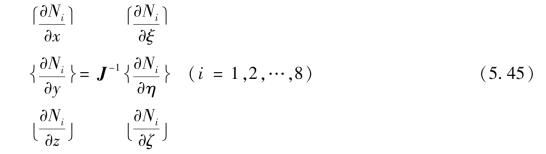
式中 J-1——雅可比矩阵的逆矩阵。
J中的各元素可由式(5.36)对坐标求导得到,即
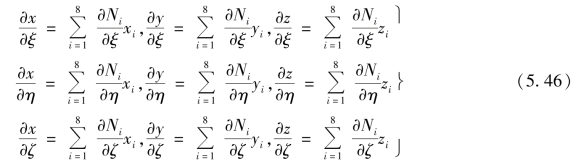
雅可比矩阵J可写为如下的矩阵形式
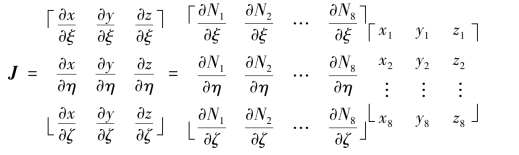
有了上述的转换公式,可求得应变矩阵B中的各元素。
下面简述式(5.40)中积分元dx dy dz的变换。
从图5.9可以看到,dξ,dη,dζ在整体坐标系内所形成的体积微元为
![]()
其中
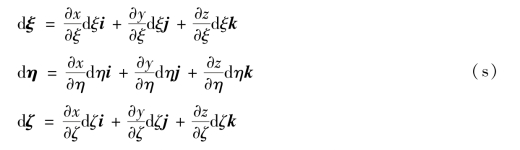
式中,i,j和k是笛卡尔坐标x,y和z方向的单位向量。将式(s)式代入式(r),得到
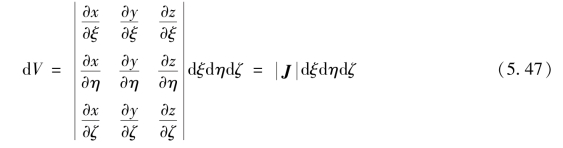
因此,单元刚度矩阵可写作
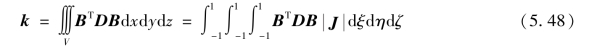
(4)单元等效荷载列阵
令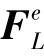 为单元等效荷载列阵
为单元等效荷载列阵
![]()
式中
![]()
由虚功方程可得单元等效荷载列阵

式中 Sσ——单元承受面力的曲面;
f——单元体力列阵;
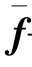 ——面力列阵。
——面力列阵。
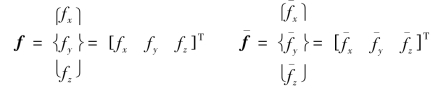
由式(5.46),故式(5.48)可写作
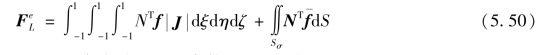
对于式(5.49)中面积微元dS,例如在ξ=c(常数)的面上有
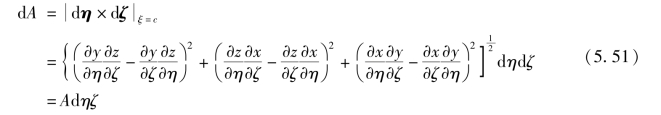
其他面上的dA可以通过轮换ξ,η,ζ得到。
单元等效荷载列阵子块