▶2.2.7 单元位移模式的收敛性准则
有限单元法是一种数值计算方法,它的计算精度应当随着网格的细化而提高。换言之,要使得弹性体网格越分越细、每个单元越来越小时,有限元解能够趋于真实解,位移模式的选取是一个关键。位移模式的设定决定了是否能通过有限单元法获得正确的解答。
研究表明,为达到这一目的,单元位移模式选择应满足如下的收敛准则。
(1)位移模式必须能反映单元的刚体位移
每个单元的位移一般总是包含着两部分:一部分是单元的形变引起的,另一部分是与本单元的形变无关的,即刚体位移,它是其他单元发生形变而连带引起的。甚至,在弹性体的某些部位,例如,接近悬臂梁的自由端处,单元的形变很小,而该单元在整体结构中的位移却很大,这主要是由于其他单元发生形变而引起的刚体位移。因此,为了正确反映单元的位移形态,位移模式必须能反映该单元的刚体位移。
(2)位移模式必须能反映单元的常应变
每个单元的应变一般总是包含着两个部分:一个部分是与该单元中各点的位置坐标有关的,是各点不同的,即所谓变量应变;另一部分是与位置坐标无关的,是各点相同的,即所谓的常量应变。而且当单元的尺寸较小时,单元中各点的应变趋于相等,因而常量应变就成为应变的主要部分。因此,为了正确反映单元的变形状态,位移模式必须反映该单元的常量应变。
上述两个条件是使得单元收敛的必要条件,也称为完备性条件,满足上述两个条件的单元称为完备单元。
(3)位移模式应当尽可能反映位移的连续性
连续性要求就是使得位移模式应当尽可能保证单元内位移的连续性和相邻单元间的公共边界上的协调性。后者表示两相邻单元在变形时既不重叠也不分离。对于梁、板和壳单元等,还要求通过公共边界时,斜率应当尽可能连续。
在连续弹性体中,为了使得单元内部的位移保持连续,必须把位移模式取为坐标的单值连续函数。为了使得相邻单元的位移保持连续,就要使它们在公共结点处具有相同的位移时也能在整个公共边界上具有相同的位移。这样就能使相邻单元在受力以后既不相互脱离、也不相互侵入,而使代替原连续弹性体的离散结构物,仍然保持为连续弹性体。因此,位移模式还应当尽可能反映出位移的连续性。
对于具体的单元以及由单元组集成的结构来说,应当明确指出:连续性是指位移函数有限阶数的导数在单元间连续。例如,对于平面的或三维应力的弹性理论问题,在变分的总势能泛函中,仅出现位移函数的一阶导数,因此,单元边界仅需要位移分量保持连续,这类问题常称为C0问题,然而,对于板和壳的问题,当应用克希霍夫(Kirchhoff)假设时,在变分的总势能泛函中出现了挠度函数的二阶函数,单元间的协调条件就要求挠度以及在公共边界上的挠度的一阶导数保持连续,这类问题常称为C1问题。
C0连续函数 (对于三维或二维弹性问题)
C1连续函数 (对于薄板弯曲问题)
满足连续性条件的单元称为协调单元。
完备协调单元可以保证其解答是收敛的;表明满足完备性与连续性是单元收敛的充分条件,即当单元越划越小时,其近似解将趋于真实解。
图2.11简单描述了单元位移模式的收敛性准则。

图2.11 单元收敛性准则(https://www.daowen.com)
需要说明的是,对于一些实际工程问题,要使得位移模式完全满足位移的协调性是比较困难的。从理论上讲,位移模式满足完备性,但不完全满足连续性条件的单元,并不能确定其一定不收敛。实际计算已有较多实例,采用完备非协调单元已经得到了令人满意的结果。
现在以常应变三角形单元(CST)为例,讨论单元的收敛性。由式(2.5),单元的位移模式为完全一次多项式
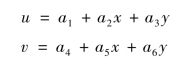
首先,考察收敛准则(1)刚体位移。为此,将上式改写为:
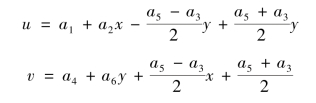
由弹性理论知:
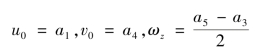
分别反映了沿x轴、y轴的刚体移动和绕z轴的刚体转动,因此,该位移模式能够反映单元的刚体位移。
其次,考察收敛准则(2)常应变。将位移函数代入几何方程(1.7)得
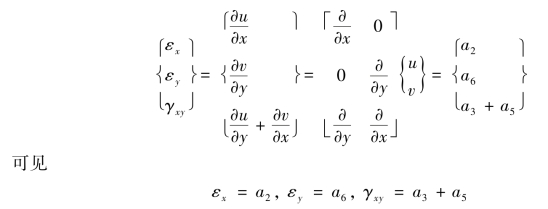
表明,常数a2,a3,a5,a6反映了常量的正应变和切应变。
由上述分析可知,3结点三角形单元为完备单元。同时表明,包含完全一次多项式的位移模式能够反映单元的完备性。反之,则无法满足完备性,因此,多项式位移模式中必须包含完全多项式。
再来考察收敛准则(3)连续性。
位移模式为多项式函数,在单元内部是单值连续的。如图2.12所示,任意两个相邻单元①、②,它们具有公共边界ij。对于单元①,位移函数为线性函数,变形过程中单元位移公共边界ij上始终保持为直线,而通过两个结点i,j的线性函数是唯一确定的。同理,对于单元②,通过两个结点i,j的线性函数也是唯一确定的。因此,弹性体变形过程中两个单元在公共边界ij上位移始终保持一致,满足连续性要求。
综上,说明三角形常应变单元为完备协调单元。
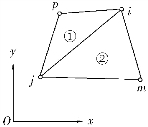
图2.12 相邻单元
