▶4.1.1　体积坐标

▶4.1.1　体积坐标

根据四面体单元的几何特点引入自然坐标系，即体积坐标。

类似于平面三角形单元的面积坐标，在三维空间的四面体中，为了避免采用行列式计算体积得到负值，结点编码1，2，3，4的排列服从右手螺旋法则。设单元体积坐标为L1，L2，L3，L4，四面体内任意点P的位置可用4个体积坐标由式（4.1）来确定，即

式中　V——四面体单元的体积；

　　　V1，V2，V3，V4——四面体P234、P134、P124、P123的体积（图4.2所示）。

由于

故有

式（4.2）表明，独立的坐标仍然为3个。

由图4.2可知，体积坐标也在各顶点上有如下特点：

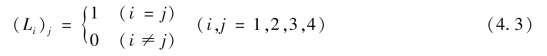
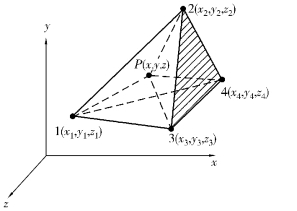
图4.2　体积坐标

4个顶点体积坐标分别为（1，0，0，0），（0，1，0，0），（0，0，1，0），（0，0，0，1）。L1在平行于结点1所对的平面234的任意平面上各点具有相同的坐标值，即L1=常数（1，2，3，4轮换）。特别的，在平面234上，L1=0（1，2，3，4轮换）。

由式（4.1）可得

式中　V——四面体的体积。

αi，βi，γi，φi为上式中行列式的代数余子式，可表示如下

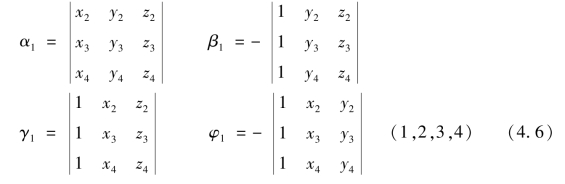
将式（4.4）写成矩阵形式

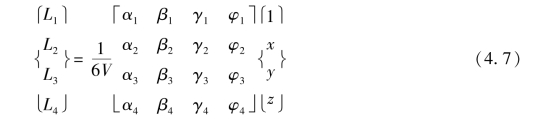
直角坐标可用体积坐标表示为

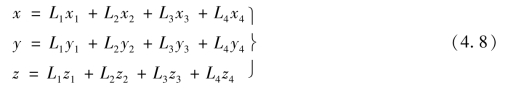
将式（4.8）连式（4.2）合并写成矩阵形式

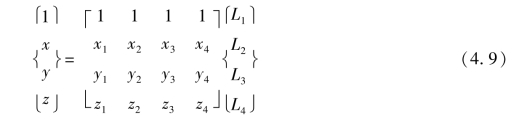
体积坐标的微分计算，采用复合函数运算法则有

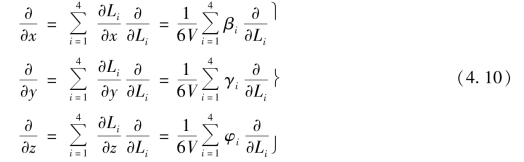
体积坐标的体积积分按照下列积分公式计算