▶3.2.1　面积坐标

▶3.2.1　面积坐标

为便于用简化计算，根据三角形几何特性，引入自然坐标系，即面积坐标L1，L2，L3。

单元任意点P（x，y）的位置可用如下3个比值来确定

式中　A——三角形单元的面积；

　　　A1，A2，A3——分别代表△P23、△P31、△P12的面积（图3.2）。

　　　L1，L2，L3表示P点位置的面积坐标，按照逆时针排序。由于

因此

式（3.2）表明，这些坐标并不是完全独立的，L1，L2，L3中只有两个线性独立的坐标。

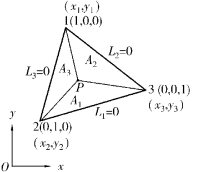
图3.2　面积坐标

不难看出，3个顶点的面积坐标分别为（1，0，0），（0，1，0），（0，0，1），L1在平行于对边23的直线上（1，2，3轮换），所有各点均具有相同的坐标值，即L1=常数。特别地，在对边23上，L1=0（1，2，3轮换）。

由图3.2，△P23的面积为

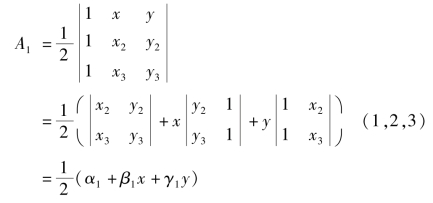
同理可得A2，A3。

统一记作

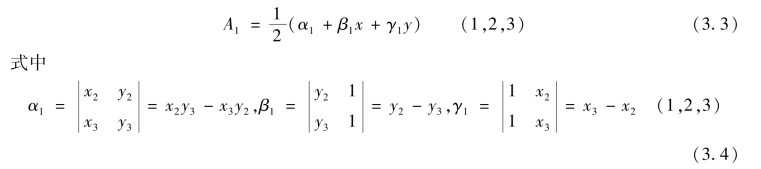
代入式（3.1），可得到用直角坐标表示面积坐标的关系式

式（3.5）写成矩阵式为

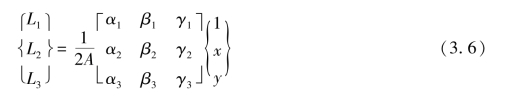
将式（3.6）中的三式分别乘以x1，x2，x3和y1，y2，y3，然后相加，并利用式（3.2），便得到用面积坐标表示直角坐标的公式

将式（3.7）与式（3.2）合并，写成矩阵式

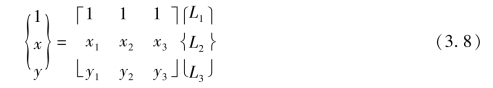
针对面积坐标的微分运算，可以采用复合函数求导法则

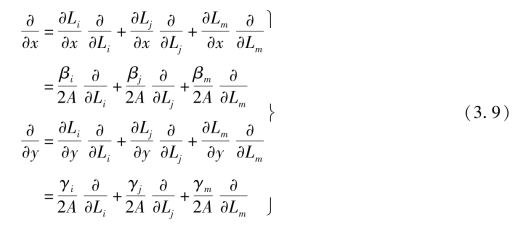
面积坐标的积分运算，可采用下列积分公式

面积坐标在三角形某一边上的积分时，可采用下列积分公式

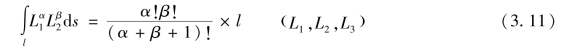
应用面积坐标可较为简单地构造高阶三角形单元的形函数。