▶6.2.2 空间杆单元
2026年01月14日
▶6.2.2 空间杆单元
与平面杆单元的刚度矩阵类似,空间杆单元的刚度矩阵也可以用局部坐标系下的单元刚度矩阵通过坐标转换来得到。这里给出另外一种方法,供参考。
如图6.3所示为一个空间杆单元,假设
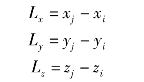
则杆长为
![]()
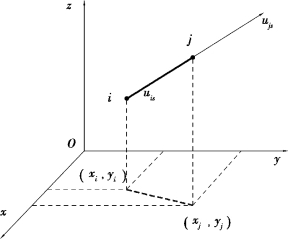
图6.3 空间杆单元
令uis,ujs分别为结点i,j的轴向位移,并假设杆的轴向位移us沿杆轴线s方向呈线性变化,则杆的轴向位移可表示为
![]()
而轴向应变为

令α,β,γ为由结点i到j的杆轴线方向分别和x,y,z轴的夹角,ui,vi,wi是结点i沿轴线方向的位移uis在总体坐标系下的位移分量,则uis可表示为
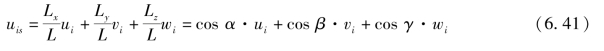 (https://www.daowen.com)
(https://www.daowen.com)
同理,若令uj,vj,wj为结点j沿轴线方向的位移ujs在总体坐标系下的位移分量,则有
![]()
将式(6.41)和式(6.42)代入式(6.39),得到
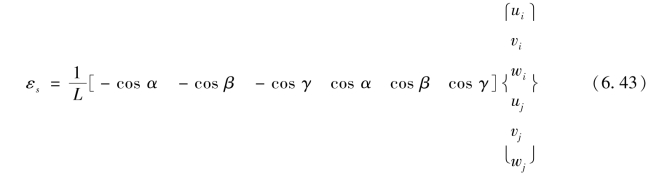
其中,B为单元应变矩阵,δe为单元结点位移列阵,即
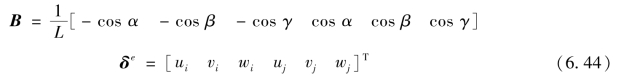
有了单元应变矩阵,就可以根据虚位移原理得到空间杆单元的单元刚度矩阵,即
![]()

式中 Ve——单元体积;
A——单元横截面面积;
L——单元长度。
