▶9.1.1　动力问题的体力表达式

▶9.1.1　动力问题的体力表达式

结构在运动中，各点除位移u以外还有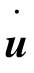速度以及加速度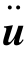。按照达朗贝尔原理，有加速度的质量应附加有惯性力荷载。如材料的密度为ρ，则结构内单位体积的惯性力为-ρ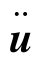，这对于结构来说，相当于又受到另一种体积分布的荷载，大小与点的加速度成正比，而与加速度方向相反。此外，在介质中运动的质点还会受到阻尼力。如阻尼系数为υ，阻尼力与速度成正比，则单位体积的阻尼力为-υ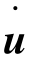。这对结构来说同样相当于有一种体积分布的荷载，大小与点的速度成正比，而与速度方向相反。

设fd为单元作用的动体力，于是，根据达朗贝尔原理则有

式中　f——单元体积上所受的体力；

　　　u——单元位移函数；

　　　ρ——材料密度；

　　　υ——阻尼系数；

　　　-——惯性力；

　　　-——阻尼力。

在有限元分析中，仍然采用与静力分析相似方法，在单元分析时，将体力等效到单元结点上，成为单元等效结点荷载；然后在整体分析时将其集成到整体荷载列阵中。