▶9.2.4 主副自由度
2026年01月14日
▶9.2.4 主副自由度
工程中结构的低阶固有频率和模态是更为重要的。
只求系统低阶部分的固有频率和模态时,还可以大力减小系统的自由度,以求简化动力计算。对具体结构,可以凭经验选出其中几个主要结点的位移作为“主自由度”,记为δa。另一部分结点位移为“副自由度”,记为δb。一般主自由度的数目可为总自由度数的![]() 。计算时,暂时先不考虑副自由度方向的质量、阻尼和荷载,只考虑主、副自由度之间的弹性联系,则式(9.19b)可简化为
。计算时,暂时先不考虑副自由度方向的质量、阻尼和荷载,只考虑主、副自由度之间的弹性联系,则式(9.19b)可简化为
![]()
这相当于一个约束方程,人为主副自由度之间必须满足式(9.21)的联系。如果δa为独立变量,δb为从属的、不独立的,则由式(9.21)可以解出
![]()
此结果与恒等式δa=δa,合在一起,有
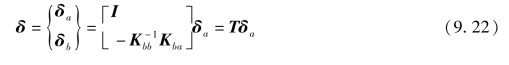 (https://www.daowen.com)
(https://www.daowen.com)
这里
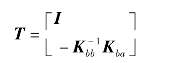
可认为是一个变换矩阵,是一个长方形矩阵,通过式(9.22),可把结点位移δ变换为更低阶的独立结点位移δa。将式(9.22)代入动力方程(9.22),并前乘以TT,有
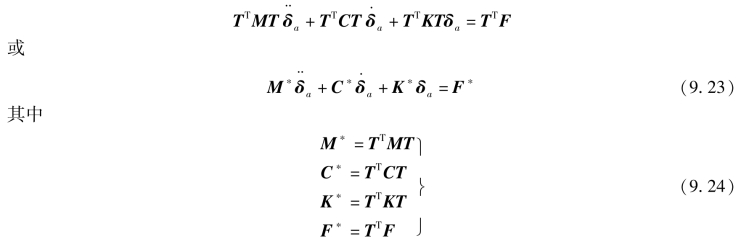
分别为变换到主自由度位移δa的相当质量、阻尼、刚度矩阵和荷载列阵。式(9.23)是一个阶数较低的动力方程,求解是比较方便的。
这里并没有完全忽略副自由度方向的质量,否则可能太过简化了;只是按没有副自由度的质量、阻尼等弹性关系式(9.9)建立变换矩阵T,而将原有的M,C,K,F等变换为低阶。
这种方法并不限于动力问题,当结构中某些结点位移之间有着某种约束时,都可以由约束方程解出不独立的部分结点位移δb,建立变换矩阵T,再变换原方程求解。
