▶1.4.3　物理方程（应力-应变关系）

▶1.4.3　物理方程（应力-应变关系）

各向同性材料线弹性体的应力与应变关系，即物理方程为

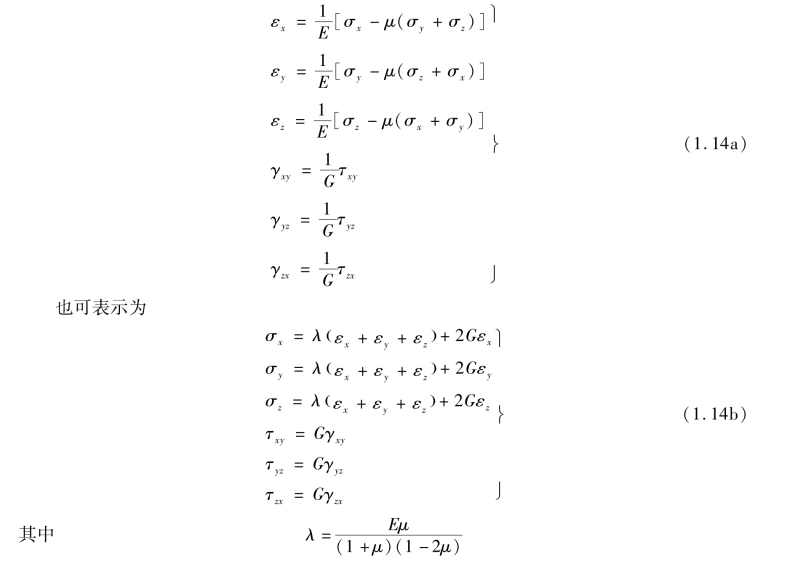
式中　λ——拉梅（Lame）常数；

　　　E——弹性模量（也称杨氏模量）；

　　　μ——泊松比；

　　　G——剪切模量，且

物理方程用矩阵表示为

式中，D为弹性矩阵

可以看到，两类平面问题其弹性矩阵是不同的。若在平面应力问题弹性矩阵式（1.18）中将E换成，μ换成，就能得到平面应变问题弹性矩阵（1.19）。

因此，设

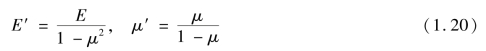
则平面应变问题弹性矩阵可表述为

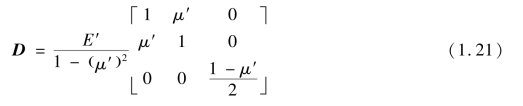
可以看出，式（1.21）与式（1.18）在形式上完全相似，故对于平面问题弹性矩阵在后续的表述中均采用式（1.18）的形式。

表1.1和表1.2分别给出了不同结构问题中对应的基本量与弹性矩阵。

表1.1　各类结构问题中对应的物理变量

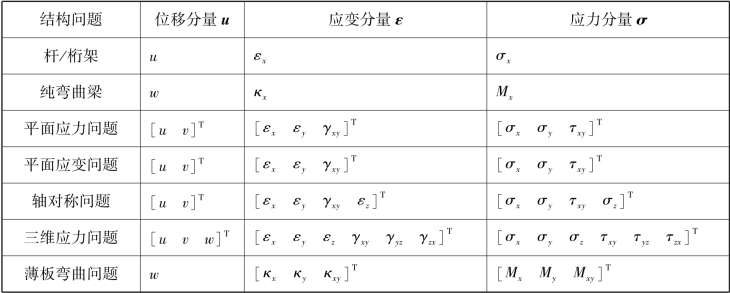
表1.2　各类结构问题中对应的弹性矩阵

续表