▶3.2.3 10结点三角形单元（三次单元）
（1）单元位移模式及其收敛性
参照Pascal三角形，三次三角形单元位移模式设为完全3次多项式：
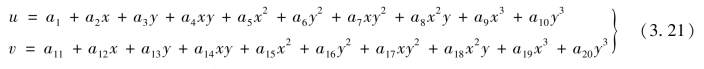
式中，u，v各有10个待定参数，按照前述分析，单元应当设置10个结点。除三角形3个角点外，考虑到相邻单元位移函数的协调性及关于坐标的对称性，在3条边的1/3长度处各设置一个结点，最后在形心处设置一个结点，该结点为内结点，如图3.5所示。
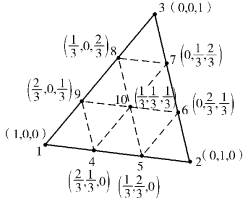
图3.5 10结点三角形单元
单元位移列阵为
式中
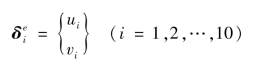
单元结点力列阵为
式中
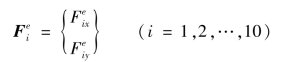
单元位移为三次函数，在边界上其位移变化形态为三次曲线，而由边界上4个结点所确定的三次曲线是唯一的，因此，可以保持相邻单元在公共边界位移的协调性。10结点三角形单元为完备协调元。
（2）构造形函数
单元位移插值函数为
按前述划线法，可直接构造其形函数。
（3）内结点聚缩过程
结点10为内结点，并不传递单元之间相互作用，在单元刚度矩阵中，可以消去，成为9结点18自由度单元，单元刚度矩阵的阶次也相应减为18×18。这一过程称为聚缩过程。
首先将刚度方程写成分块形式
式中 
为单元的边界结点位移列阵；
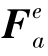为相应的结点力列阵；
δb=δ10为拟消去的内部结点位移列阵；
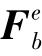为相应的结点力列阵。
将式（3.26）展开，得到：
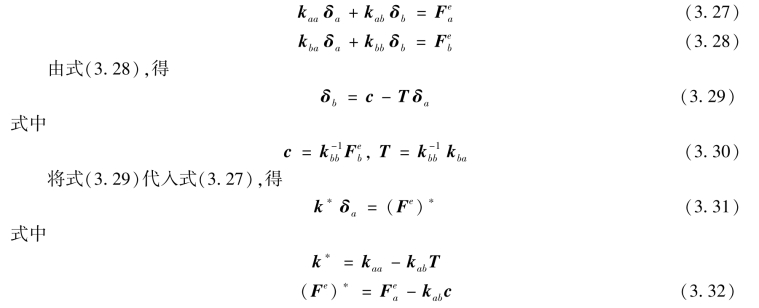
式（3.32）中kabT表示由于单元内部结点位移δb而产生的对单元刚度矩阵的修正，kabc代表由内部结点传递至单元结点的荷载。
在实际运算中，可以采用高斯消元法消去δb，从而避免矩阵求逆的复杂运算。上述内结点位移消去法也同样适用于由若干个单元组成的复杂单元，只需将复杂单元的结点位移按边界结点位移δa和内部结点位移δb重新排列即可。
单元刚度矩阵和单元等效荷载的计算可参照式（3.19）和式（3.20）。
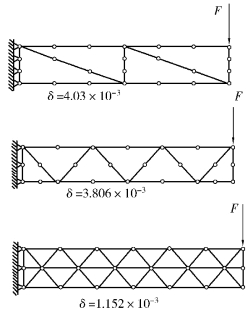
图3.6 悬臂梁挠度计算
在图3.6中表示了采用3种不同的三角形单元计算悬臂梁在集中荷载作用下的挠度。3种计算网格具有相同的结点数目。
根据位移解法的下限性质，计算的挠度是低于真实值的，因此算出的位移越大，精度越高。由图3.6可见，9结点三角形单元给出最好的结果。6结点三角形单元次之；而3结点等应变三角形单元给出的结果则较差。