▶7.2.2 单元位移模式
2026年01月14日
▶7.2.2 单元位移模式
按照位移法计算薄板时,基本未知量是位移函数w。
现在选取矩形单元的位移模式——选取单元内部各点的挠度表示式。由于矩形单元有12个自由度,因此位移模式应有12个参数。位移模式可取为多项式:
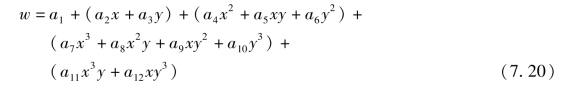
其中含有12个位移参数a1,a2,…,a12。
参照Pascal三角形,式(7.20)中包含了完全三次多项式,最后两项则是从5个四次项(x4,x3y,x2y2,xy3,y4)中选用了两项x3y和xy3。这里因坐标对称未选用x2y2项。此外也没有选用x4和y4,因为它们在矩形单元边界上给出的挠度函数是四次函数,将使相邻单元的位移连续条件更加难以满足。
式(7.20)可写成矩阵形式
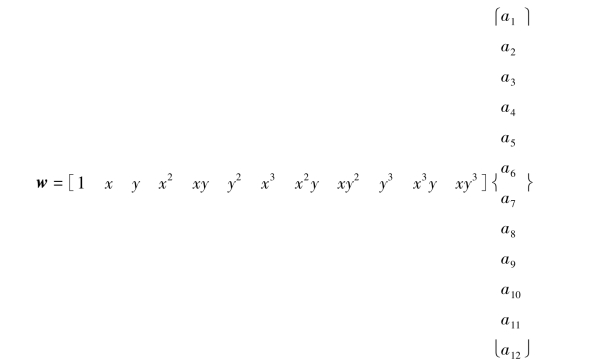
或简写为(https://www.daowen.com)
![]()
其中fw(x,y)是一个1×12阶的行向量:
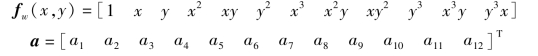
由式(7.18)可得出两个转角表示式
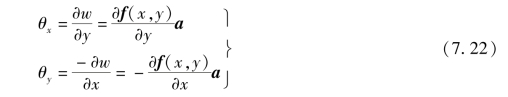
其中