▶2.3.5　整体刚度矩阵的性质

▶2.3.5　整体刚度矩阵的性质

由前面的讨论可知，总刚K是由单元刚度矩阵装配而成，它与单元刚度矩阵类同，也具有明显的物理意义。以位移为未知量的有限元的求解过程是结构离散后每个结点的平衡方程，换言之，有限元解在每个结点上是满足平衡条件的。

总刚K的任意元素Kij的物理意义是：使得整体结构结点位移列阵中第j个广义位移取单位值，而其他结点位移皆为零时，需在整体结构结点位移列阵中第i个广义位移方向上施加的广义结点力。

总刚K具备以下主要性质：

（1）对称性

整体刚度矩阵是由对称的单元刚度矩阵装配而成的，其具有对称性。因此，通常只需三角状半阵存储与计算即可。

（2）奇异性

在式（2.48）中，总刚K具有奇异性。实际上，由式（2.49）装配而成的整体结点荷载列阵FL由于约束反力的存在，整体结点荷载列阵并非完全为已知的。通过引入位移边界条件，对总刚和整体结点荷载列阵进行修正，可消除其奇异性。

（3）稀疏性

从平衡方程（2.47）可以看出，每个结点的等效结点荷载只与环绕该结点的单元有关，即只有环绕该结点的单元对该结点刚度具有贡献，这些单元称为相关单元。虽然总体结点数很多，但是每个结点的相关单元很少，这导致总刚中只有很少的非零元素，即稀疏性。

（4）非零元素带状分布

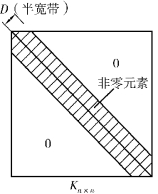
图2.15　非零因素带状分布

非零元素集中在主对角线两侧。在进行结点编码时，原则上应使相邻结点之间编码的差值尽可能小，这样得到的刚度矩阵带宽就较小。利用这个性质以及对称性，采用恰当的算法，只需按半带宽进行存储即可（图2.15），这样可以极大节省计算机存储空间。