▶5.6.3 三维高斯积分
对于三维数值积分,数值积分为
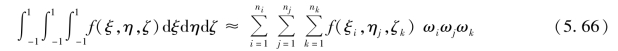
对于二维、三维数值积分,积分点数在不同的坐标方向上可以根据具体情况取不同的值。同样,如果f(ξ,η,ζ)是不高于2n-1次的多项式,则式(5.65)和式(5.66)积分的计算是精确的。
可以证明,收敛性所要求的数值积分的最低阶数,就是算出单元体积所用的阶数。也就是说最低阶数应当取决于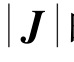 的表达式中多项式的次数。但计算实践表明,利用低阶积分法则,可以降低单元的刚度,以补偿由于假定位移场引起的结构过于刚硬的情况。各种单元的最佳积分法则通常用试凑和经验来确定。表5.3给出推荐的高斯积分计算的阶数,其在实际应用中已经证明是有效的。
的表达式中多项式的次数。但计算实践表明,利用低阶积分法则,可以降低单元的刚度,以补偿由于假定位移场引起的结构过于刚硬的情况。各种单元的最佳积分法则通常用试凑和经验来确定。表5.3给出推荐的高斯积分计算的阶数,其在实际应用中已经证明是有效的。
表5.3 等参单元高斯积分计算建议采用的阶数

【例5.2】 设N1=![]() (1+ξ)(1+η),采用高斯积分法计算
(1+ξ)(1+η),采用高斯积分法计算![]() 沿η=1的值。
沿η=1的值。
【解】 由于积分沿边界η=1,所以
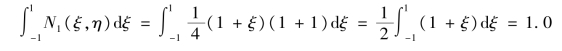
采用高斯积分法,因为被积函数为一次函数,可以取1个高斯积分点。由表5.1知,积分点坐标ξ1=0,权系数ω1=2.0,所以,
![]()
高斯积分计算结果与解析解相同。
【例5.3】 设N1=![]() (1+ξ)(1+η)(ξ+η-1),采用高斯积分法计算
(1+ξ)(1+η)(ξ+η-1),采用高斯积分法计算![]() 沿η=1的值。
沿η=1的值。
【解】 首先求解析解
![]()
采用高斯积分,因为被积函数为二次函数,可以取2个高斯积分点,即2点高斯积分,由表5.3可知,积分点坐标![]() ,权系数ω1=ω2=1.0,所以有
,权系数ω1=ω2=1.0,所以有
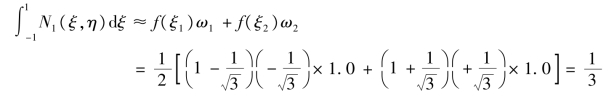
【例5.4】 如图5.11所示4结点四边形等参元,计算有限单元刚度矩阵所需的表达式。
【解】 母单元的形函数为
![]()
由坐标变换式
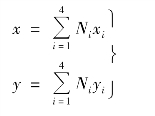 (https://www.daowen.com)
(https://www.daowen.com)
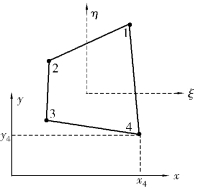
图5.11 二维4结点单元
可得到
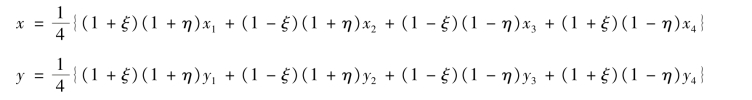
代入位移插值函数得
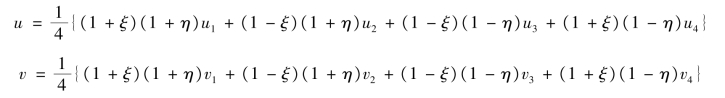
单元的应变由下式给出

因此,对于-1到1中的任意ξ和η都可以使用表达式∂x/∂ξ,∂x/∂η和∂y/∂ξ,∂y/∂η构成Jacobi算子J,假设在ξ=ξi和η=ηi处计算J,而用Jij表示算子J,det J表示行列式,则有
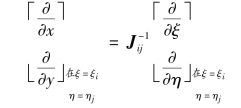
为了计算单元应变,使用如下公式
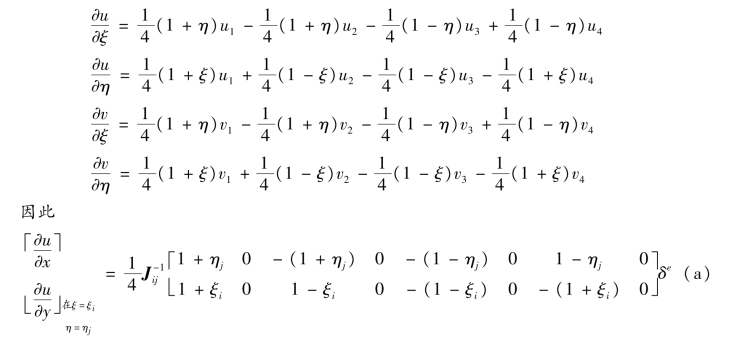
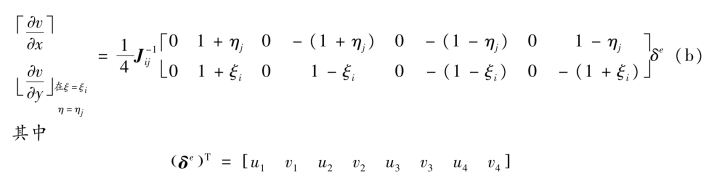
计算式(a)和式(b),可以建立点(ξi,ηj)处Bij计算的公式。例如,如果x=ξ,y=η(即一个方形单元的刚度矩阵要求边长为2),Jacobi算子是单位矩阵,因此有
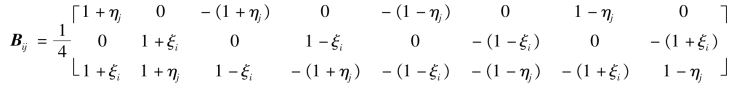
由此可得对于4结点四边形,有
![]()
F=![]() ,而积分是在单元的自然坐标下进行的。如上所述的F的元素依赖于ξ,η,但通常不计算具体的函数关系。使用数值积分,可按如下方程式计算刚度矩阵
,而积分是在单元的自然坐标下进行的。如上所述的F的元素依赖于ξ,η,但通常不计算具体的函数关系。使用数值积分,可按如下方程式计算刚度矩阵
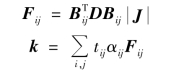
其中,tij是单元在采样点(ξi,ηj)处的厚度(在平面应变分析中tij=1.0)。在给定矩阵Fij和加权因子αij可用的情况下,能方便地计算所需的刚度矩阵。
在实际应用中,应该注意到在计算Jij,式(a)和式(b)定义的位移导数矩阵时,只需要插值函数N1,…,N4的8个可能的导数。因此,最好是开始计算Bij时就计算点(ξi,ηj)对应的导数,且在任何需要它们的时候使用即可。
