5.1 等参数单元的概念
所谓等参数单元(简称等参元),是指通过坐标变换建立的具有复杂外形的单元,且单元位移模式和坐标变换采用相同的形函数(同时参数个数相等)。对于实际物体,划分的单元可能具有曲线边界,形状比较复杂,称为子单元。在子单元中设置局部坐标系,通过整体坐标系与局部坐标系之间的转换关系,将子单元映射成局部坐标系中形状规则的单元,称为母单元。
有限单元法中对子单元的分析计算均可以转化为母单元中相对较为简便的计算,即首先导出规则单元(母单元)中的形函数;然后采用坐标变换的方法对不规则单元(子单元)进行单元分析,求出单元刚度矩阵;最后在整体坐标系下组合各子单元情况进行整体分析与求解,这就是等参数单元的基本思路,即由特殊到一般,由统一大小的、形状规则的母单元推广到一系列不规则的,大小、形状各异的子单元,从而达到简化运算、提高计算精度的目的。
等参,则是指坐标变换与位移模式的形函数阶次相等,即用以确定单元形状的结点自由度数n1等于确定单元位移的结点自由度数n2,并且坐标变换与位移函数一般采用相同的结点。若坐标变换所用形函数阶次高于位移函数中的形函数,即n1>n2,则称其为超参数单元;反之,若n1<n2,则称为逊参数单元,或称亚参数单元。
图5.1所示为两种平面单元,实际单元为图5.1(b)中的曲边四边形单元和曲边三角形单元,图5.1(a)则表示在局部坐标系中的规则单元,称作母单元。通过坐标变换,图5.1(b)中12结点曲边四边形单元映射成图5.1(a)所示局部坐标系ξ-η中边长为2×2的12结点正方形母单元;6结点曲边三角形单元则映射成图5.1(a)所示用面积坐标表示的等边三角形母单元。
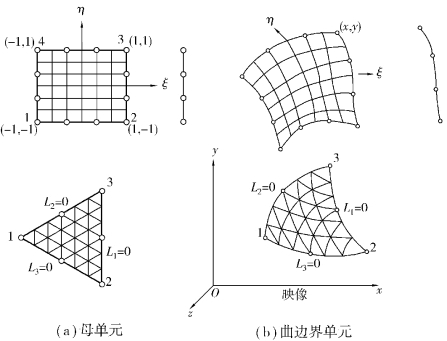
图5.1 二维等参元变换(https://www.daowen.com)
图5.2所示为两种三维空间单元,实际单元为图5.2(b)中的曲边六面体单元和曲边四面体单元,图5.2(a)则表示在局部坐标系中的规则单元,即母单元。通过坐标变换,图5.2(b)中20结点曲边六面体单元映射成为图5.2(a)中局部坐标系ξηζ中边长为2×2×2的20结点正方体母单元;10结点曲面四面体单元则映射成为体积坐标表示的10结点正四面体母单元。
等参数单元可以模拟曲线或曲面边界,适用于处理各种复杂边界的问题。同时,由于母单元形状、尺寸规整,便于函数运算,加之各种等参数单元的单元特性都同样地是由母单元分析经坐标转换导出,其推导过程具有通用性,便于计算机编程与应用。因此,等参数单元目前已广泛应用于平面问题、空间问题及板、壳等多种专题之中。
由于等参数单元中刚度矩阵和等效结点力列阵一般不能写成显式积分,计算中多采用数值积分的方法,故本章中除介绍几种常用的等参数单元之外,还简单介绍一种数值积分方法——高斯积分。
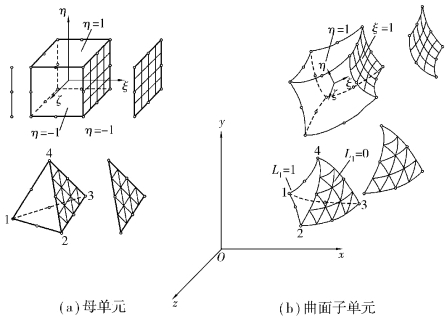
图5.2 三维等参元变换
