▶2.2.6 单元等效结点荷载
离散模型需要将所有非结点分布体力和分布面力等效移置到结点上而成为等效结点荷载。等效法则采用虚功原理,即原荷载与等效结点荷载在任意虚位移上所做的虚功相等。在给定的位移模式之下,这样移置的结果是唯一的。
设单元结点虚位移列阵为(δe)*,则单元虚位移函数为
![]()
设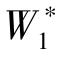 为单元体力f在单元上所做虚功
为单元体力f在单元上所做虚功
![]()
同理,可得面力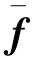 在单元上所做虚功
在单元上所做虚功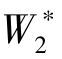
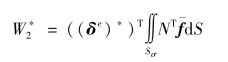
设 为等效荷载力列阵,根据虚功原理可得
为等效荷载力列阵,根据虚功原理可得
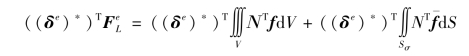
由于(δe)*为任意的,故

对于平面单元,式(2.44)可简化为

由式(2.44)和式(2.45)可以看出,单元等效结点荷载是依据单元位移形态而确定,因此,对于不同类型的单元,由于其形函数的不同,单元等效结点荷载的等效结果是不同的。
下面以简单实例计算一些常见的分布荷载产生的等效结点荷载。
【例2.1】 如图2.8所示,任一厚度为t的3结点三角形平面单元,容重为ρg,求等效结点荷载。
【解】 单元体力及面力分别为
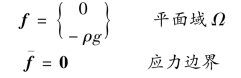
参照式(2.18),由式(2.45)可得
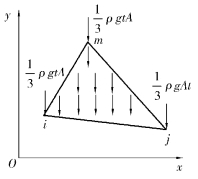
图2.8 受自重作用
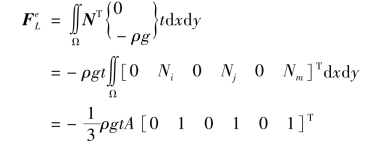 (https://www.daowen.com)
(https://www.daowen.com)
结果表明,等效结果相当于将单元总质量平均分配到3个结点上。对于常应变三角形单元,可以看出,其结果与采用静力等效平行力法则计算结果相同。
【例2.2】 如图2.9所示的3结点三角形单元,在ij边界上受x方向均布力q作用,ij边界长度为l,不计体力,求等效结点荷载。
【解】 单元体力及面力分别为
![]()
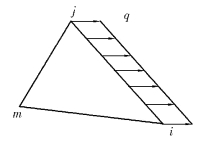
图2.9 受均布力作用

由式(2.45)可得
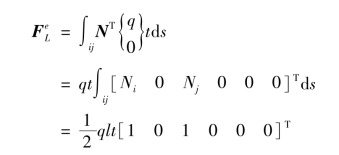
其结果表明,等效结点荷载将面力的合力平均分配到结点i和结点j上,m结点为零。对于常应变三角形单元,可以看出,其原则同样符合静力等效法则。
【例2.3】 如图2.10所示的3结点三角形单元,在ij边界上受三角形分布荷载作用,ij边界长度为l,求等效结点荷载。
【解】 为了积分方便,设从i结点出发指向j结点的直线作为局部坐标s,则ij边界在面力可表示为
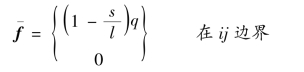
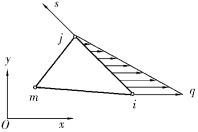
图2.10 受三角形分布荷载作用
在ij边上
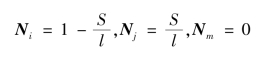
由式(2.45)可得
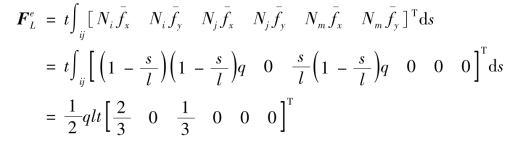
对于常应变三角形单元,其结果相当于按照静力等效法则分配到结点i与结点j。
需要说明的是,单元等效结点荷载是依据单元位移形态而确定的,上述结果仅在3结点三角形单元这种最简单的单元中得到。实际上,静力等效法则仅仅为虚功等效原则的一种特例。
