▶4.2.1 8结点六面体单元（一次单元）
如图4.8所示，任意边长为2a×2b×2c的六面体单元，选取8个角结点。
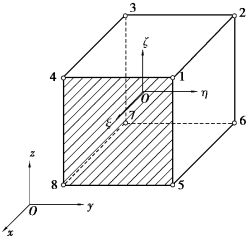
图4.8 8结点六面体单元
（1）单元位移模式
参照图4.4的Pascal三角锥，首先选择完全一次多项式，共有4个参数。其次由二次及以上的项中进行选择，由于单元各棱边各有2个结点，按照单元的收敛性要求，选择对各个坐标均为一次的3项xy，yz，zx和三次项中的xyz这一项。因此，单元位移模式设为
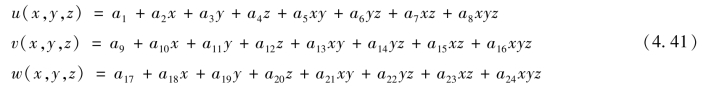
由式（4.41）可知，单元位移函数在各边界上均为x，y，或y，z，或z，x的一次方程。例如，在边界1256面（图4.7），z=常数，单元位移函数u为x，y的一次方程。
这表明在变形过程中，u保持为平面，而该平面方程可由4个结点1，2，5，6唯一确定。因此可以说明，在变形过程中，六面体单元各个边界面与相邻单元保持变形协调。
单元结点位移列阵为
式中
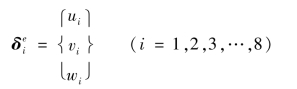
单元等效力列阵可表示为
式中
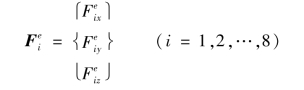
（2）局部坐标
根据六面体单元的几何特性，为便于运算，引入无量纲局部坐标系
如图4.9所示。
ξηζ与xyz坐标系之间的转换关系为
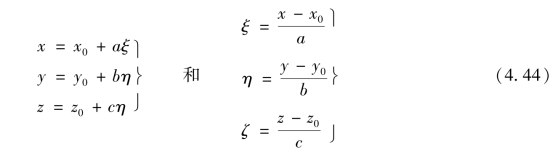
式中
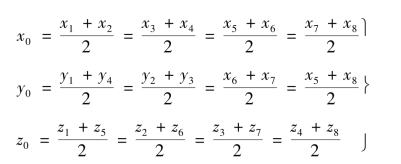
为六面体形心位置坐标。
根据复合函数微分法则，由式（3.38），式（3.39）可得
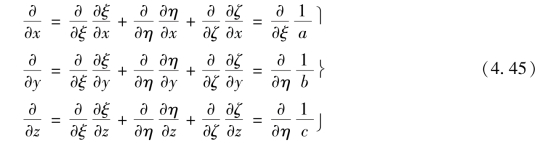
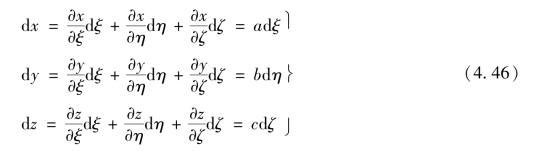
于是，通过坐标变换，任意六面体单元均可变换为边长2×2×2的正六面体单元，如图4.9所示。单元位移形函数的构造将在局部坐标系ξηζ中进行，而此形函数可映射到整体结构中所有六面体单元。
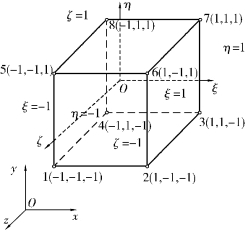
图4.9 局部坐标系下8结点六面体单元(https://www.daowen.com)
（3）单元形函数
单元插值函数可以表示为
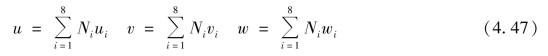
写成矩阵形式，则有
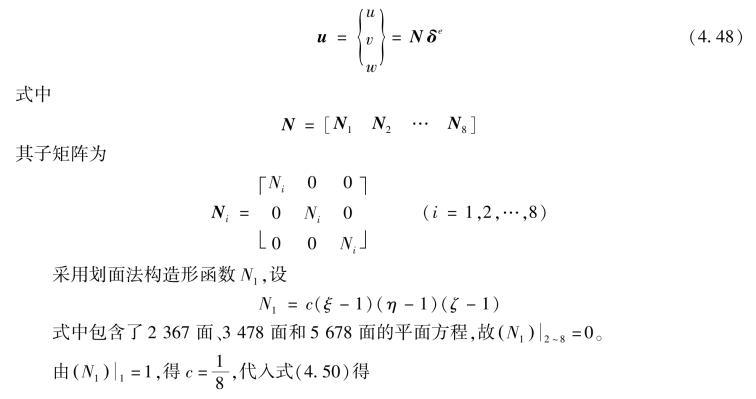
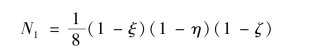
同理，可得N2～8。
写作统一格式
式中 ξ0=ξiξ，η0=ηiη，ζ0=ζiζ。
（4）单元刚度矩阵
单元刚度矩阵可表达为
式中 B——几何矩阵
其分块形式为
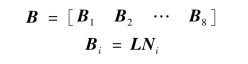
由式（4.45）得
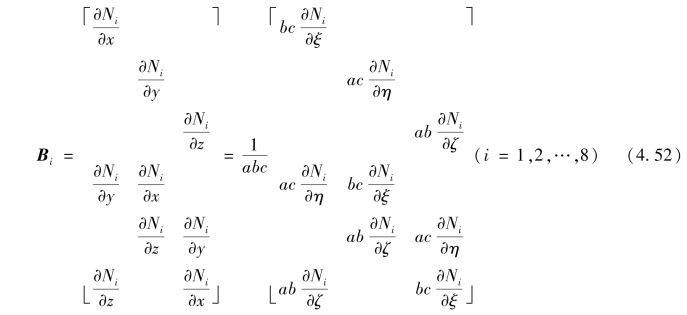
由式（4.46），式（4.50）可简化为
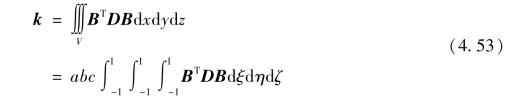
（5）等效结点荷载
设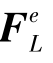
为单元等效结点荷载
三维应力单元等效结点荷载一般可表示为
式中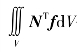 
——体力产生的单元等效结点荷载；
——面力产生的单元等效结点荷载。
由式（4.45），则得
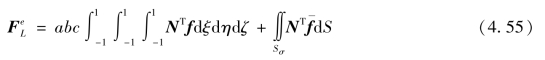
关于积分元dS，例如x=常数的面上，dS=dydz=bcdξdη。