▶4.3.1　基本方程

▶4.3.1　基本方程

在轴对称问题中，采用圆柱坐标r，θ，z比较方便。这是因为如果以弹性体的对称轴作为z轴，如图4.11所示，则所有的应力分量、应变和位移分量都将只是r和z的函数，不随θ变化。

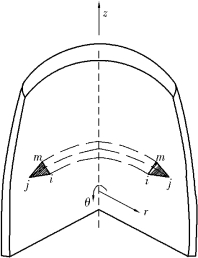
图4.11　轴对称问题

一般总是以对称轴为z轴，任意一个通过这个轴的任一平面rz面都是对称面。由对称条件可知，γrθ=γθr=0，γzθ=γθz=0，则应变分量为

式中　εr——径向正应变；

　　　εθ——环向正应变；

　　　εz——轴向正应变；

　　　γrz——切应变。

相应的应力分量为

式中　σr——径向正应力；

　　　σθ——环向正应力；

　　　σz——轴向正应力。

由对称条件可知，环向位移uθ=0，因此弹性体任意一点的位移，可以分解为2个分量：径向位移u，轴向位移w，即

由于所有的物理量均为r和z的函数，不随θ变化，因此，下面的讨论将在rz平面内进行。

根据圆柱坐标的几何关系，可以导出轴对称问题的应变-位移关系：

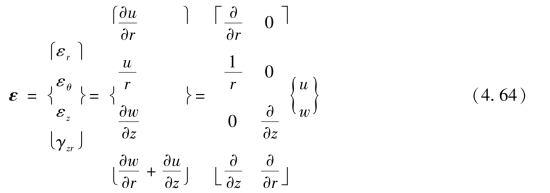
应力-应变关系可以表示为：

式中