4.5.5　二次平均法应用举例

某大学东校区××学院办公室、实验室装修工程，投标限价为168 万元（人民币，下同）。在招标机构网上发布招标公告后，共有9 家单位购买招标文件，其中7 家单位出席开标会。评标采用二次平均法，现分析其评标过程和结果。

随机抽取5 名评审专家，评审专家先对出席开标会的7 家单位进行符合性审查，主要考察各投标人的资质。招标文件规定，合格投标人注册资本必须在100 万元以上，消防施工、机电和装修各二级资质，项目经理二级资质，有B 类安全证书。经专家审查，有一家投标人的投标书正副本均没有B 类安全证书（其实在报名时已验过原件），4 名专家认为其不符合资质要求，因此根据少数服从多数的原则，共有6 家投标人符合资质要求而进入下一轮评审。根据招标文件规定，通过符合性审查的合格投标人多于6 家（含6 家，见表4-3），去掉最高报价1 617 023 元（D 投标人）和最低报价1 385 027 元（E 投标人），剩余4 家投标人的报价算术平均，得到第一次平均价1 478 299 元，然后将第一次平均价与6 个有效投标报价中最低的报价1 385 027 元再进行算术平均，得到第二次平均价1 431 663 元，第二次平均价再乘以随机抽取的浮动系数3%与1 的和（即1.03），得到评标基准价1 474 613 元，最后根据各投标报价与评标基准价的偏离程度，得到A、B、C、D、E、G 的偏离程度分别为0.765%、2.000%、－1.112%、9.657%、－6.075%和－0.652%。排名前三位的投标人依次为G、A、C，推荐为第一、第二、第三中标候选人。

表4-3　某大学东校区××学院办公室、实验室装修工程评标

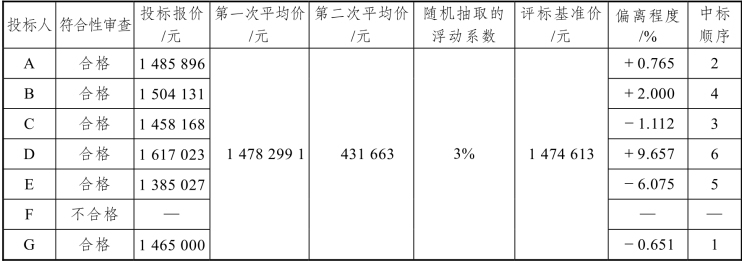
进一步分析发现，如果不设置随机抽取的浮动系数3%得到的评标基准价，而直接采取第一次平均价与最低投标价相加的算术平均值作为第二次平均价得到评标基准价1 431 663 元，则第一中标候选人为报价第二低的C 公司，符合前面关于第二次平均价中标的一般规律。因此，这个例子说明了设置随机抽取浮动系数的意义，也能成功阻止围标和猜测。同时，这个案例也说明，只要采用二次平均法，无论是否采用浮动系数，最低价中标几乎不可能。