股票内在价值计算方法
1.现金流贴现模型[2]
(1)一般公式
现金流贴现模型是运用收入的资本化定价方法来决定普通股票内在价值的方法。按照收入的资本化定价方法,任何资产的内在价值是由拥有资产的投资者在未来时期中所接受的现金流决定的。由于现金流是未来时期的预期值,必须按照一定的贴现率返还成现值。也就是说,一种资产的内在价值等于预期现金流的贴现值。对股票而言,预期现金流即为预期未来支付的股息。因此,贴现现金流模型的一般公式如下:

式中:V为股票在期初的内在价值;Dt为t时每股股息;k是必要收益率。
根据上式,可以引出净现值(NPV)的概念。净现值等于内在价值与成本之差,即:
![]()
式中:P为在t=0时购买股票的成本。
如果NPV>0,意味着所有预期的现金流入的现值之和大于投资成本,即这种股票被低估价格,因此购买这种股票可行。如果NPV<0,意味着所有预期的现金流入的现值之和小于投资成本,即这种股票价格被高估,因此不可购买这种股票。
(2)内部收益率
内部收益率是指使得投资净现值等于零的贴现率。如果用k*代表内部收益率,根据内部收益率的定义可得下式:

即:

由此可见,内部收益率实际上是使得未来股息流贴现值恰好等于股票市场价格的贴现率。
由上述(8.10)式可以解出内部收益率k*。将k*与具有同等风险水平股票的必要收益率k相比较:如果k*>k,则可以考虑购买这种股票;如果k*<k,则不要购买这种股票。
运用现金流贴现模型决定普通股票内在价值存在一个困难,即投资者必须预测所有未来时期支付的股息。由于普通股票没有一个固定的生命周期,通常要给无穷多个时期的股息流加上一些假定,以便于计算股票的内在价值。这些假定始终围绕着股息增长率g。
2.零增长模型
零增长模型假定股息增长率等于零,即g=0。也就是说,未来的股息按一个固定数量D0支付。零增长模型公式为:(https://www.daowen.com)

3.不变增长模型
不变增长模型可以分为两种形式:一种是股息按照不变的增长率增长,另一种是股息以固定不变的绝对值增长。相比之下,前者比后者更为常见。因此,我们主要对股息按照不变增长率增长这种情况进行介绍。
如果我们假设股息永远按不变的增长率增长,假设时期t的股息为:
![]()
就可以建立不变增长模型。

例如,去年某公司支付每股股息为1.80元,预计在未来日子里该公司股票的股息按每年5%的速率增长。因此,预期下一年股息等于1.80×(1+0.05)=1.89(元)。假定必要收益率是11%,根据不变增长模型(8.13)式可知,该公司股票的价值等于:
1.80×(1+0.05)÷(0.11-0.05)=1.89÷(0.11-0.05)=31.50(元)
若当前每股股票价格是40元,股票被高估8.50元,投资者应该出售该股票。
零增长模型实际上是不变增长模型的一个特例。假定增长率g等于零,股息将永远按固定数量支付,这时,不变增长模型就是零增长模型。
从这两种模型来看,虽然不变增长的假设比零增长的假设有较小的应用限制,但是在许多情况下仍然被认为是不现实的。但由于不变增长模型是多元增长模型的基础,因此这种模型是极为重要的。
4.可变增长模型
零增长模型和不变增长模型都对股息的增长率进行了一定的假设。事实上,股息的增长率是变化不定的,因此,零增长模型和不变增长模型并不能很好地在现实中对股票的价值进行评估。下面,我们主要对可变增长模型中的二元增长模型进行介绍。
二元增长模型假定在时间L以前,股息以一个g1的不变增长速度增长;在时间L后,股息以另一个不变增长速度g2增长。在此假定下,我们可以建立二元可变增长模型:
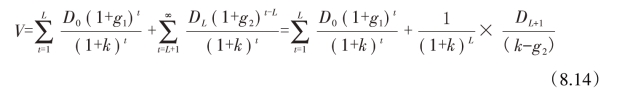
式中:DL+1=D0(1+g1)t×(1+g2)。
若某公司目前股息为每股0.2元,预期回报率为16%,未来5年中超常态增长率为20%,随后的增长率为10%,即D0=0.2,g1=0.20,g2=0.10,L=5,k=0.16,代入公式(8.14)得:该公司股票的理论价值为5.45元。当市场价格高于5.45元时,投资者应该出售该股票;反之,则投资者应该买进该股票。
与二元增长模型相类似,我们还可以建立三元等多元增长模型,其原理、方法和应用方式与二元增长模型差不多,投资者可以根据自己的实际需要加以考虑。
