波浪理论中的比率与周期分析
1.波浪理论中的比率
比率分析是波浪理论中一个浪与另一个浪在价格波动幅度上的比例关系。比率分析有助于我们正确地认识、区别每一浪。波浪理论的使用者相信，每一浪的幅度都可以按斐波那契数列中的某个比率与相邻波浪的长度计算得到。一个在波浪中经常出现的反映精确价格关系的数字，主要有两类比率关系：回落或反弹关系和倍数关系。
（1）回落或反弹
在计算回落或反弹幅度时要考虑浪的位置，这对于高低点的确定有一定的指导作用。通常，一个调整的回落或反弹幅度是前面波浪的斐波那契百分比。如图10-42所示，一般的调整经常回落至前面波浪的61.8%以下的位置，剧烈的调整要回落到前面主浪的38.2%的位置。回落以各种规模出现，图中的这些比率仅仅是一种倾向。如果稍加留意就可以发现，这里的做法与百分比线中的两个点的黄金分割线的做法是基本一致的。反弹的分析大体也相同。
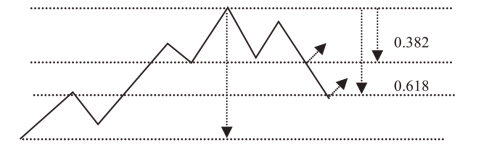
图10-42 波浪理论的回落或反弹
（2）波浪长度的倍数关系
1）推动浪长度之间的比率关系
第一，如果推动浪中的一个子浪成为延伸浪的话，则其他两个推动浪不管其运行的幅度还是运行的时间，都将趋向于一致或成0.618的倍率关系。例如，如果第3浪是延伸浪，那么第1浪和第5浪就趋向于升幅并且运行时间会大致相同。假如升幅和运行时间并非完全相等，则它们极有可能以0.618的关系相互维系。第二，第5浪的长度与第1浪至第3浪的长度（第1浪高点至第3浪高点）呈斐波那契比率关系。如果第5浪是延伸浪，则这一比率关系可能是1.618。当第5浪不延伸的时候，这样的倍数关系可能是0.382或0.618。
2）调整浪之间的比率关系
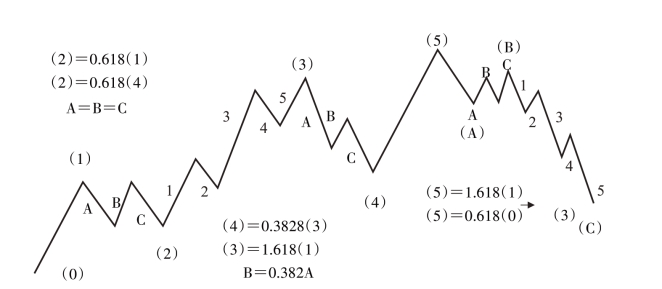
波浪理论中调整浪长度之间的比率关系呈现出以下的特点。①锯齿形调整浪。C浪的长度与A浪长度之间有3种可能的倍数关系：等长（1倍）、1.618倍和0.618倍，经常是1.618倍。②平台形调整浪。在最规则的常规平台形中，A浪和C浪的长度当然相等。在扩散形平台中C浪的长度通常是A浪的1.618倍，在少数情况下会出现相等。在扩散形平台中C浪的长度通常是A浪的1.618倍，在少数情况下会出现2.618倍的情况。③三角形调整浪。在进行三角形调整时，各浪之间的关系也涉及黄金比例。如果三角形最宽处的第一次调整的高度是h，那么，其后的相反方向的第二次调整的高度应该是0.618h。应该注意，确定三角形每次调整的起点和终点是很困难的。正是由于这个原因，三角形各调整浪之间的长度比率的实用性受到了很大的影响。④第4浪与第2浪的价格波动范围相等，或成黄金比例的关系，如图10-43所示。
图10-43 波浪长度的倍数关系
常见的比率关系有以下9个：
浪（2）＝0.618×浪（1）；
浪（3）＝1.618×浪（1）；
浪（4）＝0.382×浪（3）；
浪（5）＝1.618×浪（1）；
浪（5）＝0.618×浪（0）→（3）；
浪（2）＝0.618×浪（4）；
在浪（2）中，（A）＝（B）＝（C）；
在浪（4）中，（A）＝（C），（B）＝0.236×（A）。
2.波浪理论中的时间周期分析
这个问题实际上涉及循环周期理论。在波浪理论中，对时间因素的考虑体现在每个浪所运行的时间长短上，如完成某个浪所要经过的交易日或交易周。就目前而言，在中国还没有比较得到共同认可的结论。初步的结论是，完成某个浪所要经过的时间，一般是斐波那契数列中的某个数字。从对1994年以前的上证指数的具体研究中可以发现，局部低点和高点之间的时间以21周、13周居多。