三、行为组合模型

行为组合模型（Behavior Portfolio Theory，简称BPT）模型是由斯塔曼和谢弗林（Shefrin ＆ Statman）在行为金融理论的研究成果和资产组合理论（APT）的基础上发展起来的。在APT模型中，投资者通常假定他们始终都是风险厌恶者，并将资产作为整体来考虑，且仅仅考虑不同证券之间的协方差。在BPT模型中，投资者具有金字塔形层状结构的资产组合，资产组合金字塔的每一层都对应着投资者的特定投资目的和风险特性（方差）。金字塔是在与安全性、潜力性和期望收益这三者相关的投资需求上构建起来的。金字塔的底部是为投资者提供安全性而设计的证券，包括货币市场基金和银行存款保证；往上一层是债券，投资者需要把某些特定的投资用于某些特定的目标，例如：使用零息债券去实现准备供养孩子上大学的目标；再上一层是股票和房地产。金字塔结构从底部到顶部是按其风险程度由低到高排序的，从右到左则是按其收入价值由低到高排序的。

谢弗林和斯塔曼认为，行为投资组合的构建要考虑5个主要因素。一是不同层的投资分配取决于投资者的目标和目标的重要性。例如，假设第一个投资者认为投资组合要有上升潜力是最重要的投资目标，而第二个投资者认为潜在损失最小化是最重要的目标，那么，对于最高上升潜力层的资金分配，第一个投资者要大于第二个投资者。二是层内的资金分配到特定资产将取决于该层设定的目标。目标越高，则该层选择的资产风险越大，投机性越强。三是层内选择的资产数量取决于投资者效用函数的形状。风险厌恶的投资者的效用函数是凹函数，这意味着财富的边际效用是递减的。效用曲线的弧度越大，投资者在该层选择的证券种类就越多。四是如果投资者认为他们拥有某些证券的私人信息，那么他的资金可能集中分配于这些证券中。五是不愿意确认损失的投资者可能持有数量更多的现金，这样他们就不必通过出售可能处于亏损状态的证券来满足流动性需求。此外，这些投资者之所以持有某些证券，可能不是因为这些证券具有增长潜力，而是因为投资者不喜欢确认损失。虽然这使得他们的投资组合看起来多样化，但实际上，从均值方差的角度来看，它们的组合可能不是有效率的。

弗里德曼和萨维奇（Friedman＆Savage）认为，一个人购买保险的同时又购买彩票，是明显不合理的行为。谢弗林和斯塔曼应用行为组合模型对这类看似不合理的行为进行了解释。在行为组合理论中，投资者最大化预期财富的同时，又不想让自己的财富受到太多的损失。在这样的目标背景下，对于极小的概率才能实现的财富水平，虽然最终目标没有达成，但投资者是可以接受的。换句话说，投资者构建特定投资组合，在保证自身财富不受过大损失的同时最大化预期财富。因此，行为组合模型中的投资者的最佳投资组合是债券或无风险资产与高投机资产的组合。也就是说，行为投资组合中投资者基本上都会构建一个类似于保险和彩票的投资组合。

对于金字塔形层状结构的资产组合，在最底层，投资者通过购买债券或无风险资产以确保他的目标财富的安全；在第二层，投资者愿意用剩余财富追求风险。因此，在行为投资组合理论中，投资者的最优投资组合可能不同于基于均值方差理论的理性投资组合。

假定两个行为符合行为投资组合理论的投资者正在构建投资组合。他们的投资组合最多包含3层：第一层是无风险投资，第二层是风险适度的投资，第三层是高风险投机投资。无风险投资层（第一层）的预期回报率是1%。适度风险投资层（第二层）的预期回报率为－3%的概率是10%，预期回报率为5%的概率为80%，预期回报率为9%的概率为10%，故适度风险投资层的总体预期回报率为4.6%。投机投资层（第三层）预期回报率为－50%的概率为15%，预期回报率为12%的概率为50%，预期回报率为75%的概率为35%，故投机投资层的总体预期回报率为24.75%。

第一个投资者A有2000元，且其财富的期望水平也是2000元，概率为100%。换句话说，投资者A不会容忍任何财富损失。第二个投资者B也有2000元，其财富的期望水平是2100元，概率为80%，且投资者B不能容忍他的投资组合财富水平下降到1800元以下。基于上述描述，我们可以为每个投资者构建他们的最优行为投资组合。

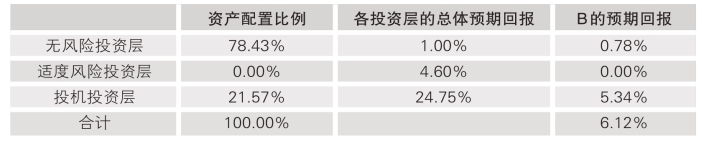
鉴于投资者A无法忍受任何财富损失，A的投资组合是将100%投入无风险投资层中。投资者B的期望回报率为5%，高于适度风险投资层4.6%的总体预期回报，故在配置B的资产时主要考虑无风险投资层和投机投资层。鉴于B的安全财富水平为1800元和投机投资层的最大可能损失为50%，投资者可在第一层投入大约1568.63元，占比78.43%，在第三层投入431.37元占比为21.57%。这样的资产配置可以保证即使投资投机层发生了最严重的50%的资产损失，B的资产仍然会有1800元（1568.63×1.01＋431.37×50%）。从表12-3可以发现，这一投资组合将会给投资者B带来6.12%的总体预期回报。

表12-3　投资者B的资产配置与预期回报

进一步考虑这样的资产配置能否满足投资者B要求的投资组合有80%的概率至少为2100元。结合投机投资层的投资状况，我们可以发现这个投资组合的最终价值为1800元（1568.63×1.01＋431.37×50%）的概率是15%，价值为2067.45元（1568.63×1.01＋431.37×1.12）的概率是50%，价值为2339.22元（1568.63×1.01＋431.37×1.75）的概率是35%。尽管这样的投资组合满足了投资者B的财富安全目标，但投资组合没有达到投资者的期望财富水平。投资组合的价值有85%的概率至少为2067.45元，而不是以80%的概率至少为2100元。考虑到投资者的风险承受能力，投资者可以决定接受这样的投资组合，或者可以考虑降低他的安全财富水平。