1.1.4 位置矢量运动学方程
物理学中有许多不同的物理量。既有大小又有方向的物理量叫作矢量;只有大小而没有方向的物理量叫作标量,如质量、时间等。矢量和标量运算法则截然不同。标量的运算方法是代数法,矢量的运算方法是几何法,即平行四边形法则。矢量必须由大小和方向同时确定,两个矢量相等必须是大小相等且方向相同。标量仅由大小确定,两个标量只要大小相等,则两个标量就相等。关于矢量代数的基本知识,请参见附录。
运动总是和时间相联系的。不同时刻质点的位置和速度都可能不同,也即运动随时间而变化。从数学上看,描述运动的物理量可以表示成以时间为自变量的函数。
要描述一个质点的运动,首先要确定质点相对于参考系的位置。可以在参考系上取一点O称之为原点,从原点O到质点所在位置P点的有向线段能唯一地确定质点相当于参考系的位置。从原点O到质点所在位置P点的有向线段r叫作位置矢量,简称位矢。它是矢量,有大小和方向。位置矢量的大小r代表质点到坐标原点的距离,位置矢量的方向标志了质点的位置相对于原点的方向。
从图1.2中可以看出,位矢r在x轴、y轴和z轴上的投影(即质点的坐标)分别为x、y和z。所以,质点在直角坐标系中的位置既可以用位置矢量r来表示,也可以用坐标x、y和z来表示。因此,位置矢量r也可写成
![]()
其中,i、j、k为沿三个坐标轴方向的单位矢量(大小为1,仅表示方向)。x、y、z称为位置矢量r的三个分量,分量是标量,有大小和正负号。位置矢量r的大小为
![]()
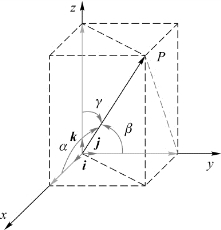
图1.2 质点的位置矢量
位置矢量r的方向可用方向余弦来表示,方向余弦由下式确定:
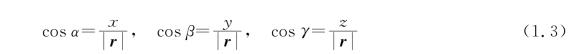
当质点运动时,它相对坐标原点O的位置矢量r随时间变化。因此,r是时间的函数,它在三个坐标轴上的投影也是时间的函数,即(https://www.daowen.com)
![]()
式(1.4)叫作质点的运动方程或运动函数。式(1.4)也可以用分量式表示:

式(1.5)叫作运动学方程的分量式。
质点运动时所经过的空间点的集合称为轨迹(或轨迹曲线)。描写此曲线的数学方程叫作轨迹方程。在运动方程的分量式中消去时间t就得到轨迹方程。由数学概念可知,运动方程的分量式也就可以称为质点运动轨迹的参数方程。
例1.1 已知一质点的运动方程为r(t)=at i+(bt-ct 2)j,a、b、c为常量。求该质点的轨迹。
解 在任一时刻t,该质点的坐标:
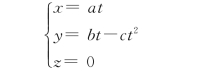
由第3个公式可知,质点在x Oy平面内运动。由第1个公式可解得t=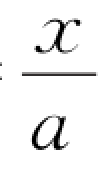 ,代入第2个公式得这就是该质点的轨迹方程,它是在x Oy平面内经过原点O的抛物线。
,代入第2个公式得这就是该质点的轨迹方程,它是在x Oy平面内经过原点O的抛物线。
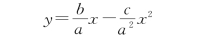
研究质点的运动方程时,坐标系的选择是任意的,主要依研究问题的方便而定。选择的坐标系不同,描述物体运动的方程也不同,但对物体运动的规律是没有影响的。质点运动方程包含了质点运动中的全部信息,是解决质点运动学问题的关键所在。因此,运动学的重要任务之一就是找出各种具体运动所遵循的运动方程。
