4.4.1　质点系的功能原理

4.4.1　质点系的功能原理

根据质点系的动能定理,有

因此,内力有保守力和非保守力之分。如以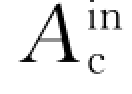表示质点系内各保守内力做功之和,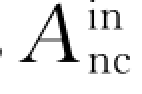表示质点系内各非保守内力做功之和,那么质点系内一切内力所做的功应为

此外,从式(4.22)可知,系统内保守力做的功等于势能增量的负值,因此质点系内各内力的保守力所做的功应为

考虑了以上两点,质点系的动能定理可写为

在力学中,动能和势能统称为机械能,即

E=E k+E p

若以E 0和E分别代表质点系的初机械能和末机械能,那么式(4.27)可写成

式(4.28)表明,质点系机械能的增量等于外力与非保守内力做功之和。这就是质点系的功能原理。

功能原理是从动能定理中推得的,无非是用势能代替内保守力的功,两者无本质区别。但这在对能量的认识上又进了一步,我们引入了机械能——动能和势能之和,这是力学中所涉及的能量的一种形式,引入机械能更能从“能”的角度来讨论问题。另外,用功能原理在计算上更为简单,因为势能比内保守力的功易于计算。但需要注意,应用功能原理,右边为机械能的增量,左边是外力和非保守内力的功;而用动能定理,右边是动能的增量,左边则是外力、保守内力、非保守内力的功。不要在应用功能原理时,把势能增量和保守内力的功重复计算进去。

功能原理指出,机械能的增量用外力和非保守内力的功来量度;动能定理指出,动能的增量用外力和一切内力的功来量度;而势能的增量用内保守力的功来量度。其实质均是用功来量度能量的变化,这使我们更加理解“功”这个概念——功是能量变化的量度。