1.2.1 直线运动
所谓直线运动是指质点运动的轨迹是直线。在这种情况下,我们将坐标系的一个坐标轴建立在该直线轨迹上,就能够使数学处理大大简化。因为当一个坐标轴建立在该运动直线上时,所有描述运动的物理量的其他坐标分量都为零而不需要做任何计算和处理,只有一个坐标分量需要计算和处理。通常情况下,如果质点在水平方向上做直线运动,我们就将x轴建立在运动直线上,这时描述运动的物理量都只有x分量。在直线运动中,位移、速度、加速度都在一条直线上。所以在研究直线运动时,有关的物理量都可以用标量表示,用正、负号表示它们的方向。正号表示沿坐标轴正向,负号表示沿坐标轴反向。
![]()
图1.7 直线运动
设质点沿x轴做直线运动,坐标轴原点为Ο(图1.7)。显然质点的坐标x是随时刻t而改变的,x为正值时表示质点的位置在原点的右边;x为负值时表示质点的位置在原点的左边。其质点运动方程为
![]()
位移为
![]()
速度为

加速度为

上述公式是直线运动中的基本公式。在上述结论中,v和a的正负可以表明方向。例如,v为正表明速度的方向与x轴的正向一致;v为负表明速度的方向与x轴的负向一致。
例1.5 已知质点的运动方程x=5-6t+3t 2,式中t以s计,x以m计。试求:
(1)质点在第2秒末的速度和加速度;
(2)质点在前2秒内的位移和路程。
解 对运动方程x=5-6t+3t 2求导数,可得速度和加速度分别为(https://www.daowen.com)
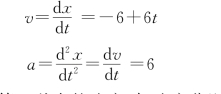
(1)将t=2 s代入以上两式得第2秒末的速度、加速度分别为
v 2=-6+6×2=6 m/s
a 2=6 m/s2
(2)根据位移的定义有
Δx=x 2-x 0
而x 0=5 m,x 2=5-6×2+3×22=5 m,则
Δx=x 2-x 0=0
当求前2秒内的路程时,应考虑在此时间内质点运动的速度是否变向。若速度方向不变,则路程与位移大小相等。若速度变向,则先令v=0,解出反向点,再分段计算总路程。此时路程和位移不再相等。
在t=0时,此时质点位于图1.8中的A点。由于加速度与v 0反向,速度肯定要变向,令v=0,得t=1 s,代入运动方程得反向点坐标x 1=2 m(B点)。因加速度不变,所以从1 s以后,质点将沿x正向做初速度为零的匀加速直线运动,且在t=2 s时,质点又回到A点。由图1.8可得质点在前2秒内的路程为
x 0=5 m, v 0=-6 m/s, a=6 m/s2
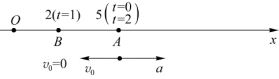
图1.8 例1.5用图
s=2×(5-2)=6 m
注意:在运动学这部分内容当中,在二维和三维坐标系中位矢、位移、速度和加速度这些物理量的标量式符号都是该物理量的大小,本身不含正负号。特别地,对于一维直线运动,为了使数学表达更加简洁,位矢、位移、速度和加速度的标量式符号本身包含正负号,通过正负号来表示方向。
