1.1.6 速度
1.平均速度和平均速率
位置矢量描述质点某时刻的位置,位移描述某时间间隔内质点的位置变化,但不能描述位置变化的快慢。因此需要引进一个新的物理量。
若质点在一较短时间间隔t→t+Δt内完成位移Δr,那么这段时间内质点位置平均变化的快慢可以记为
![]()
称为质点在Δt时间内的平均速度。它是一个矢量,方向与位移的方向相同。
在描述质点运动时,也常用到“速率”这个概念。若质点在Δt时间内走过的路程是Δs,那么Δs与时间Δt的比值叫作质点在Δt时间内的平均速率,记为
![]()
平均速度与质点的位移和所用的时间有关。因而在叙述平均速度时,必须指明是哪一段时间内或哪一段位移内的平均速度。平均速率是一个标量。不能把平均速度和平均速率等同,例如,质点经过一个闭合的路线,平均速度是零,但平均速率却不为零。
2.瞬时速度
在t→t+Δt内,平均速度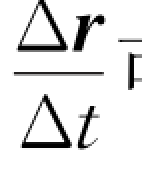 可近似地描述t时刻附近质点运动的快慢和方向。显然,Δt取得越短,近似的程度就越好,平均速度就越能反映出t时刻的真实运动情况。当Δt趋近于零时
可近似地描述t时刻附近质点运动的快慢和方向。显然,Δt取得越短,近似的程度就越好,平均速度就越能反映出t时刻的真实运动情况。当Δt趋近于零时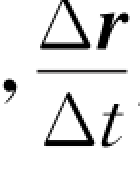 趋近于一个确定的极限矢量,这个极限矢量确切地描述了质点在t时刻运动的快慢和方向。因此,我们把这个极限矢量定义为质点在t时刻的瞬时速度,简称速度,记作
趋近于一个确定的极限矢量,这个极限矢量确切地描述了质点在t时刻运动的快慢和方向。因此,我们把这个极限矢量定义为质点在t时刻的瞬时速度,简称速度,记作
![]()
在数学中,上述极限值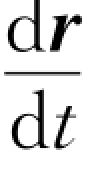 即为位置矢量对时间的一阶导数。在物理意义上,
即为位置矢量对时间的一阶导数。在物理意义上,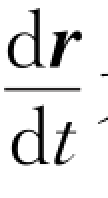 为位置矢量r随时间的变化率。因而质点在t时刻的瞬时速度v也就是在该时刻位置矢量r随时间的变化率。
为位置矢量r随时间的变化率。因而质点在t时刻的瞬时速度v也就是在该时刻位置矢量r随时间的变化率。
速度在直角坐标系下的矢量式为
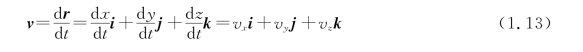
标量式为(https://www.daowen.com)

速度的大小为
![]()
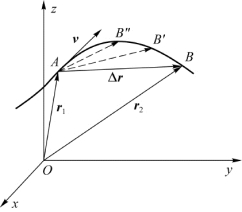
图1.4 速度
速度是矢量,它的方向即Δt趋近于零时Δr的极限方向。从图1.4中可以看出,Δt→0时Δr趋于轨道在A点的切线方向。所以我们说,速度的方向是沿着轨道的切向,且指向前进的一侧。速度的方向也可以用方向余弦来描述,方向余弦可根据矢量运算的一般方法由速度的三个分量确定。质点的速度描述质点的运动状态,速度的大小表示质点运动的快慢,速度的方向即为质点的运动方向。
对平均速率取Δt→0的极限,即为瞬时速率,简称速率,即

因为Δt→0,Δs=Δr ,Δt永远是非负数,所以有
![]()
速度的大小就等于速率的大小。在国际单位制中,速度的单位是m/s(米/秒)。
从上面的讨论可知,当我们说到速度时,必须想到它描述的是质点在某一时刻t的瞬时运动状态。一般来说,速度是可以随时间变化的,即
v=v(t)
因为v是矢量,所以函数v(t)既包括了速度大小的变化,也包括了速度方向的变化。
在不同的参考系中,同一质点的速度是不同的。
