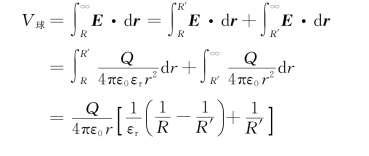6.3* 电介质中的高斯定理
根据真空中的高斯定理,通过闭合曲面S的电场强度通量为闭合曲面所包围的电荷除以ε0,即
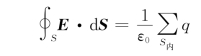
![]()

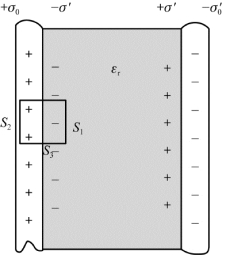
图6.18 有介质时的高斯定理
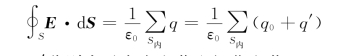
其中,q 0、q′分别表示自由电荷和极化电荷。
下面以平行板电容器为例来讨论。如图6.18所示,设极板上自由电荷面密度为±σ0,介质在极板分界面上极化电荷面密度为±σ′,介质相对介电常数为εr。实际上,q′难以测量和计算,故应设法消除。
介质内电场E=E 0+E′,由于E 0与E′方向相反,可得
![]()
由此可见,在电介质内部合场强总是小于自由电荷产生的电场强度,即
E′<E 0
可得
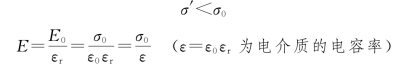
即
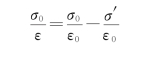
可得

束缚电荷与极化电荷的关系为

取柱形高斯面,底面S 1、S 2分别在介质和极板内,且与板面平行,S 3为侧面,与板面垂直。此时,由高斯定理知,
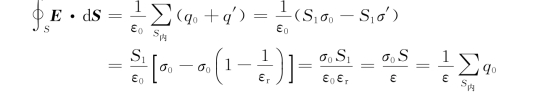
可得
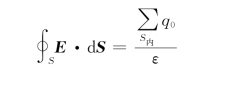
由上可知,q′不出现了。定义:(https://www.daowen.com)
![]()
其中,D称为电位移矢量(注意:此式只适用于各向同性电介质)。
高斯定理为
![]()
式(6.4)为电介质中的高斯定理,它是普遍成立的。D是辅助量,无真正的物理意义。算出D后,可求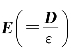 。
。
如同引进电场线一样,为了描述方便,可引进电位移线,并规定电位移线的切线方向即为D的方向,电位移线的密度(通过与电位移线垂直的单位面积上的电位移线条数)等于该处D的大小。所以,通过任一曲面上的电位移线条数为∫S D·d S,称其为通过S的电位移通量;对于闭合曲面,电位移通量为∮S D·d S。可见,有介质存在时,高斯定理为:电场中通过某一闭合曲面的电位移通量等于该闭合曲面内包围的自由电荷的代数和。
电位移线与电场线有区别:电位移线总是始于正的自由电荷,止于负的自由电荷(从定理可以看出);而电场线是可始于一切正电荷和止于一切负电荷(即包括极化电荷)。例如,平行板电容器的情况(不计边缘效应),如图6.19所示。
引入了电位移这一辅助物理量,有电介质的高斯定理数学表达式中只有自由电荷这一项,这样处理电介质中的电场问题就比较简单,可以避开束缚电荷,求出D,然后求E=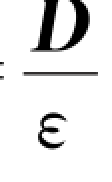 。
。
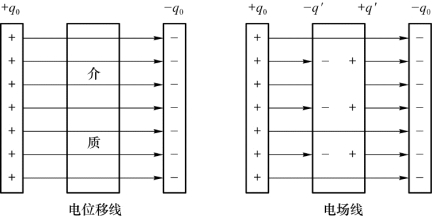
图6.19 电位移线和电场线
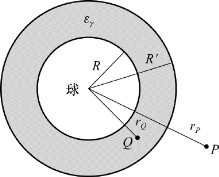
图6.20 例6.4用图
因为
所以
例6.4 如图6.20所示,在半径为R的金属球外,有一外半径为R′的同心均匀电介质层,其相对介电常数为εr,金属球电量为Q,试求:
(1)场强的空间分布;
(2)电势的空间分布。
解 (1)由题意知,场强是球对称的,取球形高斯面S,由![]() 有
有
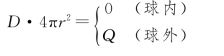
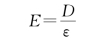

方向为:Q>0,E沿半径向外;Q<0,E沿半径向内。
(2)介质外任一点P的电势为
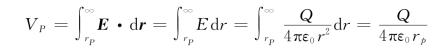
介质内任一点Q的电势为
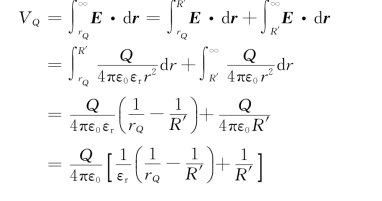
球为等势体,电势为