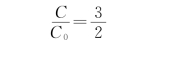6.4.2　电容器

6.4.2　电容器

1.电容器的电容

实际上,孤立的导体是不存在的,周围总会有别的导体,当有其他导体存在时,则必然因静电感应而改变原来的电场分布,影响导体电容。下面我们具体讨论电容器的电容。

两个带有等量异号电荷的导体所组成的带电系统称为电容器。电容器可以储存电荷,下文将看到电容器也可以储存能量。

如图6.21所示,两个导体A、B放在真空中,它们所带的电量分别为+q、-q,如果A、B电势分别为V A、V B,那么A、B之间的电势差为V A-V B,电容器的电容定义为

若将B移至无限远处,V B=0,上式就是孤立导体的电容。孤立导体的电势相当于孤立导体与无限远处导体之间的电势差。所以,孤立导体电容是B放在无限远处时的特例。导体A、B常被称为电容器的两个电极。

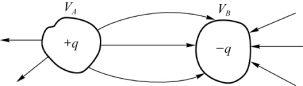
图6.21　电容器

2.电容器电容的计算

(1)平行板电容器

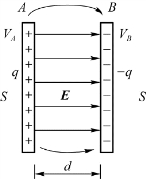
图6.22　平行板电容器

这种电容器由中间充满电介质的两块平行金属极板组成。如图6.22所示,设A、B两极板平行,面积均为S,相距为d,电量为+q、-q,极板线度比d大得多,且不计边缘效应,所以A、B间为均匀电场。

由高斯定理知,A、B间场强的大小为

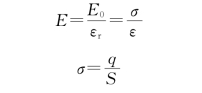
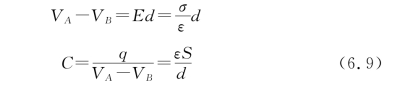
可见,平行板电容器的电容仅与电容器的形状、尺寸、电介质有关,与极板的面积成正比,与极板间的距离成反比。

增大电容的方法有:

①插入纸片、陶瓷等;

②增大极板面积,但该方法成本高。

(2)球形电容器

这种电容器由两个同心金属球壳组成,两球壳之间充满电介质(图6.23)。设有两均匀带电同心球面A、B,半径分别为R A、R B,电荷为+q、-q。分析:电场只分布在两极板之间,A、B间任一点场强的大小为

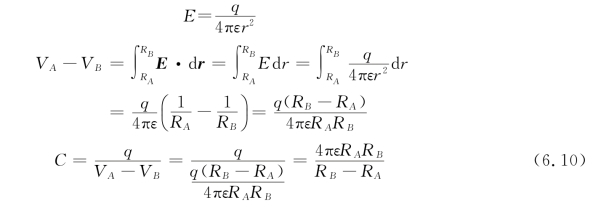
下面讨论两种极端情况:

①当两个半径都很大,且RB-R A≪R A时,有RB≈R A,令R B-RA=d,则这就是平行板电容器电容的表达式。

②当外半径R B远远大于内半径R A时,外球壳在无穷远处,有

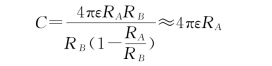
这就是半径为R A的孤立导体球在电介质中的电容。

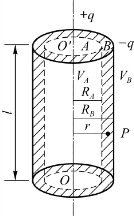
(3)圆柱形电容器

圆柱形电容器是两个同轴柱面极板构成的。如图6.24所示,设A、B半径为R A、RB,电荷为+q、-q,除边缘外,电荷均匀分布在内外两圆柱面上,单位长柱面带电量λ=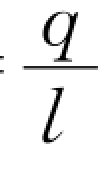,l为柱高。

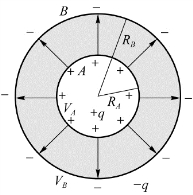
图6.23　球形电容器

(https://www.daowen.com)

图6.24　圆柱形电容器

由高斯定理知,A、B内任一点P处E的大小为可见,圆柱形电容器的电容取决于长度、内外半径的比值以及电介质的电容率。

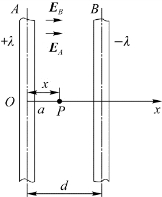
图6.25　例6.5用图

综上,电容只与电介质、电容器的形状和大小有关,与带电量无关。

例6.5 如图6.25所示,半径为a的两平行长直导线相距为d(d≫a),二者电荷线密度为+λ、-λ,试求:

(1)两导线间的电势差;

(2)此导线组单位长度的电容。

解 (1)如图6.25所示选取坐标系,P点场强大小为

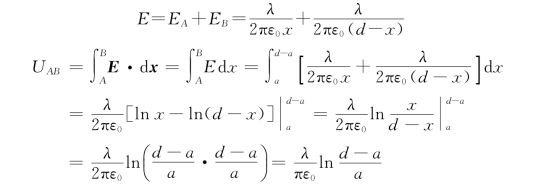
(2)

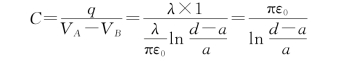
计算电容的一般步骤如下:

①设电容器两极板带有等量异号电荷q;

②求两极板之间电场的分布,先求真空中的电场E 0,再用E=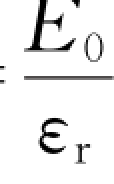求介质中电场分布;

③计算两极板之间的电势差

④根据电容器电容定义计算电容。

例6.6 如图6.26所示,面积为S的平行板电容器两板间距为d,求:

(1)插入厚度为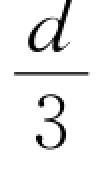、相对介电常数为εr的电介质,其电容变为原来的多少倍?

(2)插入厚度为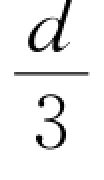的导电板,其电容变为原来的多少倍?

解 (1)如图6.25(a)所示,电介质外的场强为E 0=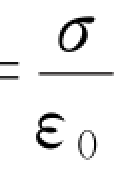,而电介质内的场强为E r=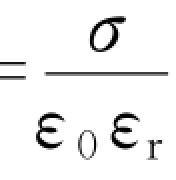,所以两板间的电势差为

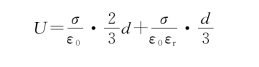
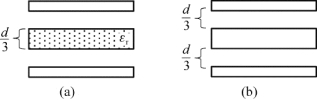
图6.26　例6.6用图

那么

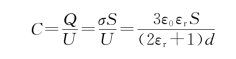
而C 0=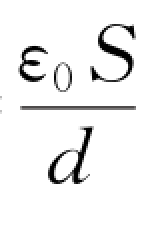,所以

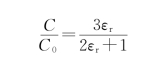
(2)插入厚度为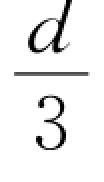的导电板,如图6.25(b)所示,可看成是两个电容的串联,有

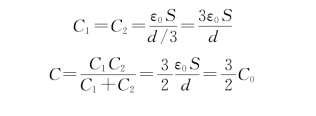
可得