7.4.1 安培环路定理
静电场中的电场线不是闭合曲线,电场强度沿任意闭合路径的环流恒等于零,即∮L E·d l=0。这是静电场的一个重要特征。但是在磁场中,磁感应线都是环绕电流的闭合曲线,因而可预见磁感应强度的环流∮L B·d l不一定为零:如果积分路径是沿某一条磁感应线,则在每一线段元上的B·d l都大于零,所以∮L B·d l>0。这种环流可以不等于零的场叫作涡旋场。磁场是一种涡旋场,这一性质决定了在磁场中不能引入类似电势的概念。
在真空中,各点磁感应强度B的大小和方向与产生该磁场的电流分布有关。可以预见环流∮L B·d l的值也与场源电流的分布有关。下面的定理将给出它们之间十分简单的定量关系。
为简单起见,下面从特例计算环流∮L B·d l的值,然后引入定理。
1.闭合圆形路径包围单根载流导线
设真空中有一长直载流导线,它所形成的磁场的磁感应线是一组以导线为轴线的同轴圆(图7.11),即圆心在导线上,圆形磁感应线所在的平面与导线垂直。在垂直于长直载流导线的平面内,任取一条以载流导线为圆心、半径为r的圆形环路L作为积分的闭合路径,则在这圆周路径上的磁感应强度的大小为B=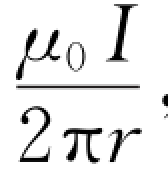 ,其方向与圆周相切。如果积分路径的绕行方向与该条磁感应线方向相同,也就是积分路径的绕行方向与包围的电流成右手螺旋关系,则B与d l间的夹角处处为零,于是
,其方向与圆周相切。如果积分路径的绕行方向与该条磁感应线方向相同,也就是积分路径的绕行方向与包围的电流成右手螺旋关系,则B与d l间的夹角处处为零,于是
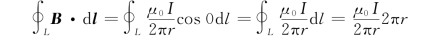
所以
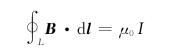
上式说明,磁感应强度B的环流等于闭合路径所包围的电流与真空磁导率的乘积,而与积分路径的圆半径r无关。
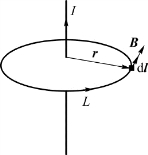
图7.11 闭合圆形路径包围单根载流线
如果保持积分路径的绕行方向不变,而改变上述电流的方向,由于每个线元d l与B的夹角θ=π,则
B·d l=B cosθd l=-B d l<0
所以
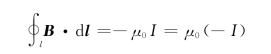
上式说明,积分路径的绕行方向与所包围的电流方向成左旋关系,可认为对路径来讲,该电流是负值。
2.任意闭合回路包围单根载流导线
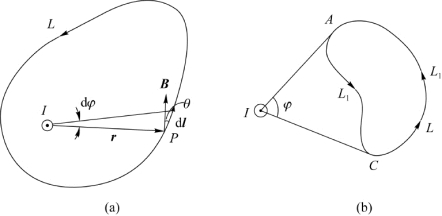
现在垂直于电流的平面内围绕电流取一任意形状的闭合路径L(称为安培环路),如图7.12(a)所示。考虑回路L上任一线元d l,磁感应强度B与d l的标积为
B·d l=B d l cosθ=Br dφ
又由于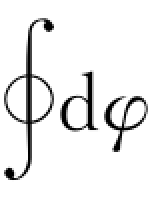 =2π,有
=2π,有
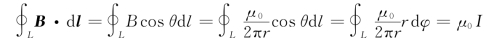
即
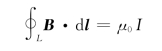
 (https://www.daowen.com)
(https://www.daowen.com)
图7.12 任意闭合回路包围单根载流导线与不包围单根载流导线
3.在垂直平面内的任一闭合路径L不包围电流
如图7.12(b)所示,如果闭合路径L不包围电流,则从L上某点出发,绕行一周后,φ的变化为零,即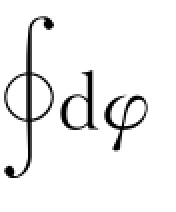 =0,因而有
=0,因而有
![]()
4.围绕多根载流导线的任一回路
设电流I 1,I 2,…,In穿过回路,电流In+1,In+2,…,In+k不穿过回路。令B 1,B 2,…,B n+k分别为单根导线产生的磁场,则有
即
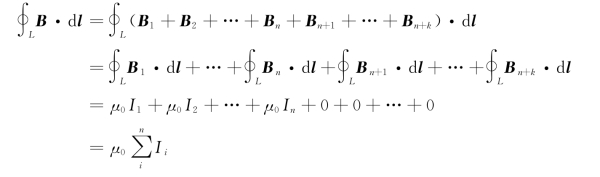
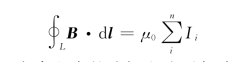
由此,总结出安培环路定理:在真空中的稳恒电流磁场中,磁感应强度B沿任意闭合曲线的线积分(也称B的环流),等于穿过该闭合曲线的所有电流强度(即穿过以闭合曲线为边界的任意曲面的电流强度)代数和的μ0倍,即
![]()
电流I正负的规定:I与L成右手螺旋关系时,I为正;反之为负。如图7.13所示,由三根载流导线与回路l关系有
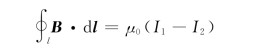
如果L不是平面曲线,载流导线不是直线,上式也成立。安培环路定理只说明∮L B·d l仅与L内的电流有关,而与L外的电流无关,但B是L内、外所有电流共同产生的结果。
安培环路定理反映了磁场的基本规律。和静电场的环路定理∮l E·d l=0相比较,恒定磁场中B的环流∮L B·d l≠0,说明恒定磁场的性质和静电场不同,静电场是保守场,恒定磁场是非保守场。
例7.5 如图7.14所示,求∮L B·d l。
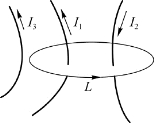
图7.13 多根载流线与任一回路
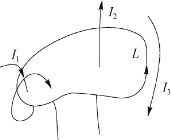
图7.14 例7.5用图
解 由安培环路定理有
![]()
需要说明的是,闭合路径L“包围”的电流,指的是与L相铰链的电流。若闭合回路与数匝电流铰链,如图7.14所示,I 1有两匝电流与回路L铰链,则计算被包围电流时应被看成2I 1。
