3.4 质点的角动量定理和角动量守恒定律
2026年01月14日
3.4 质点的角动量定理和角动量守恒定律
两个矢量A和B的矢积定义为一个矢量C,写作
C=A×B
C的大小为
C=AB sinθ
其中,A、B分别为矢量A和B的模,θ为矢量A和B之间小于180°的夹角。
C的方向满足右手螺旋定则,即伸开右手,四指从A沿小于180°的角转向B,拇指所指的方向即是C的方向。如果以矢量A和B组成平行四边形的邻边,则C垂直于平行四边形所在的平面,C的大小等于平行四边形的面积,如图3.14所示。(https://www.daowen.com)
根据定义,有
A×B=-B×A
研究物体的运动时,人们经常遇到质点或质点系绕某一确定点或轴线运动的情况,并且在这类运动中也存在着某些共同的重要规律。对于这种运动,可以用角动量来描述其运动状态,本节引入一个新的物理量——角动量来描述质点相对于某一参考点的运动状态,更有利于揭示这类运动的规律性。例如,天文观测表明,行星绕太阳运动遵从开普勒第二定律,在近日点附近绕行速度较快,远日点速度较慢,这个特点如果用角动量及其规律很容易说明。特别是在有些过程中,动量和机械能都不守恒,却遵守角动量守恒定律,这就为求解这类运动问题开辟了新途径。
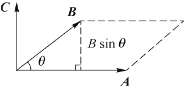
图3.14 矢积
角动量不但能描述经典力学中的运动状态,在近代物理理论中也是表征微观运动状态的重要物理量,如原子核的角动量,通常称为原子核的自旋,就是描写原子核特性的。
