12.1 黑体辐射
1900年4月27日,在英国皇家学会迎接新世纪的年会上,著名物理学家开尔文做了展望新世纪的发言。他回顾了过去的岁月,并充满自信地说:物理学的大厦已经建成,未来的物理学家只需要做些修修补补的工作就行了。只是晴朗的天空中还飘着两朵乌云,一朵与黑体辐射有关,另一朵与迈克尔逊实验有关。
然而,不到一年的时间(1900年年底),第一朵乌云就带来了量子论,紧接着(1905年),第二朵乌云带来了相对论。经典物理学的大厦被彻底地动摇了,物理学发展到了一个全新的、更为广阔的领域。
物体加热时发出的光的颜色有随温度而改变的现象。例如,当加热铁块时,开始看不出它发光。随着温度的不断提升,铁块逐渐变得暗红、赤红、橙色而最后成为黄白色,这似乎说明物体在不同温度下能发出不同频率的电磁波。然而,事实上(严格的实验已经证明),物体在任何温度下都向外发射各种频率的电磁波,只是在不同的温度下所发出的各种电磁波的能量按频率有不同的分布,所以才表现为不同的颜色。这种能量按频率的分布随温度而不同的电磁辐射称为热辐射。
为了定量地研究物体热辐射的规律,引入光谱辐射出射度的概念。光谱辐射出射度(按频率分布)用Mν表示,频率为ν的光谱辐射出射度定义为单位时间内从物体单位表面积发出的频率在ν附近单位频率区间的电磁波的能量,它的国际单位是W/(m2·Hz)。实验测得100 W白炽灯钨丝表面在2 750 K时以及太阳表面的Mν和ν的关系如图12.1所示(图中钨丝和太阳的Mν的标度不同)。从图上可以看出,钨丝发的光的绝大部分能量在红外区域,而太阳发的光中可见光占相当大的成分。
物体在向外辐射电磁波的同时,还吸收照射到它表面的电磁波。如果在同一时间内从物体表面辐射的电磁波的能量和它吸收的电磁波的能量相等,物体和辐射就处于温度一定的热平衡状态,这时的热辐射称为平衡热辐射。下面只讨论平衡热辐射。
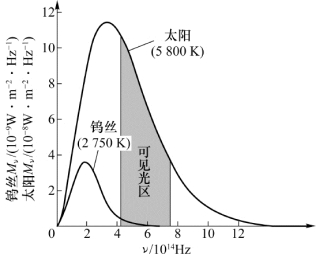
图12.1 钨丝和太阳的Mν和ν的关系曲线
在温度为T时,物体表面吸收的频率在ν到ν+dν区间的辐射能量占全部入射的该区间的辐射能量的份额,称为物体的光谱吸收比,用α(ν)表示。实验证明,辐射能力越强的物体,其吸收能力也越强。理论上可以证明,尽管不同材料的Mν和α(ν)可以有很大的差别,但在同一温度下二者的比值Mν/α(ν)却与材料种类无关,是一个确定的值。能完全吸收照射到它上面的各种频率的光的物体叫作黑体。对于黑体,α(ν)=1,因此它的光谱辐射出射度应是各种材料中最大的,并且只与温度和频率有关。所以,研究黑体辐射的规律就具有更基本的物理意义。
另外,对黑体辐射的研究在物理学史上还曾具有重要的现实意义。在19世纪下半叶的欧洲,德国(普鲁士)赢得了普法战争的胜利,急于从一个以农业为主的“土豆王国”变成一个工业化的“钢铁王国”,因此急需提高冶炼技术。炼钢的关键是控制炉温,而对于数千摄氏度的炉温,在当时任何的温度计都会被融化。于是人们希望从钢水的颜色来辨认温度,这就依赖对热辐射和黑体辐射的研究。而早已完成工业革命的英国也在不断改进炼钢技术,因此许多英国科学家和德国科学家一样,也致力于黑体辐射的研究。
如图12.2所示,不管用什么材料制成一个空腔,如果在腔壁上开一个小洞,则射入小洞的光就很难有机会再从小洞出来了。这样的一个小洞实际上就能完全吸收各种波长的入射电磁波而形成一个黑体。加热这个空腔到不同的温度,小洞就成了不同温度下的黑体。用分光技术测出由它发出的电磁波的能量按频率的分布,就可以研究黑体辐射的规律了。
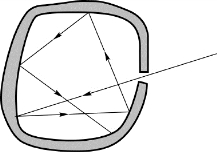
图12.2 黑体模型
19世纪末,实验物理学家通过精巧的实验测出了黑体的Mν和ν的关系曲线,于是就有人试图从理论上加以解释。1896年,维恩从经典热力学和麦克斯韦分布律出发,导出了一个公式,称为维恩公式,即
Mν=αν3 e-βν/T
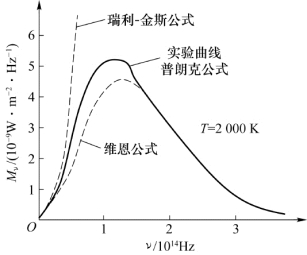
其中,α和β为常量。维恩公式给出的结果在高频范围和实验结果符合得很好,但在低频范围有较大的偏差(图12.3)。
 (https://www.daowen.com)
(https://www.daowen.com)
图12.3 黑体辐射的实验和理论结果的比较
1900年,瑞利根据经典电磁学和能量均分定理导出了一个公式,后来由金斯加以修正,称为瑞利-金斯公式,即
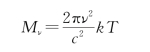
瑞利-金斯公式给出的结果在低频范围内还能符合实验结果,但在高频范围就和实验结果相差甚远,甚至趋向无穷大(图12.3)。在黑体辐射研究中出现的这一经典物理理论的失效,在当时被物理学家惊呼为“紫外灾难”。这也就是开尔文在迎接新世纪的年会上所说的第一朵乌云。
1900年12月14日,普朗克发表了他导出的黑体辐射公式,即普朗克公式:这一公式给出的结果在全部频率范围内都与实验结果相符(图12.3)。在高频范围内,普朗克公式转化为维恩公式;在低频范围内,普朗克公式则转化为瑞利-金斯公式。
![]()
此外,从普朗克公式出发还可以导出当时已被证实的两条实验定律。一条是关于黑体的全部辐射出射度的斯特藩-玻尔兹曼定律:
![]()
其中,σ称为斯特藩-玻尔兹曼常量,其值为σ=5.670 51×10-8 W/(m2·K4)。另一条是维恩位移律:在温度为T的黑体辐射中,光谱辐射出射度最大的光的频率νm由下式决定:
νm=CνT
其中,Cν为一常量,其值为Cν=5.880×1010 Hz/K。维恩位移律说明,随着温度的升高,νm向高频方向“位移”。这些结果进一步证明了普朗克公式的正确性。
普朗克之所以能够导出他的公式,是由于他做了能量量子化的假设。当时人们认为辐射体由大量谐振子(如分子、原子或其他抽象的东西)构成。吸收辐射,谐振子振动就加强;释放辐射,谐振子振动就减弱。物理学家以谐振子为基础来构造辐射模型。对于空腔黑体的热平衡状态,普朗克认为是组成腔壁的带电谐振子与腔内辐射交换能量而达到热平衡的结果。他大胆地假定谐振子可能具有的能量不是连续的,而是只能取一些离散的值。用E表示一个频率为ν的谐振子的能量,普朗克假定
E=nhν
其中:n为大于等于零的整数;h为一常量,后来就叫作普朗克常量,它的现代最优值为h=6.626 075 5×10-34 J·s。
普朗克把每一个hν给出的能量值称为一个“能量子”,这是物理学史上第一次提出量子的概念。但普朗克本人在提出量子概念之后,还长期试图用经典物理来解释它的由来,但都失败了。直到1911年,他才真正认识到量子化的全新的、基础性的意义,它是根本不能由经典物理导出的。由于量子这一概念的革命性和重要意义,普朗克获得了1918年的诺贝尔物理学奖。
