9.2.1 杨氏双缝干涉实验
19世纪初,托马斯·杨首先用实验方法研究了光的干涉现象。这是最早利用单一光源形成两束相干光,从而获得干涉现象的典型实验。
杨氏双缝实验如图9.12(a)所示,由光源发出的单色光照射在狭缝S上(S相当于光源)。在S前放置两个相距很近的狭缝S 1和S 2,S 1、S 2与S平行,且与S等距离。根据惠更斯原理,S 1、S 2形成两个新的相干光源,因为它们是同一光源S形成的,满足振动方向相同、频率相同、位相差恒定的相干条件,故S 1、S 2为相干光源。这样,由S 1和S 2发出的光波在空间相遇,将产生干涉现象。如果在S 1和S 2的前面放置一屏幕E,则屏幕上将出现等间距的明暗相间的干涉条纹,如图9.12(b)所示。
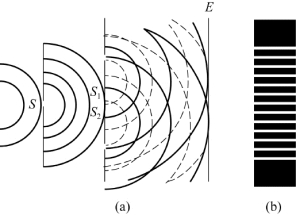
图9.12 杨氏双缝干涉实验
下面我们定量地讨论一下屏幕E上干涉条纹的分布及出现明暗条纹应满足的条件。如图9.13所示,设S 1和S 2间距为d,双缝与屏幕E间的距离为D,D≫d。在屏幕上的任取一点P,它与S 1和S 2的距离分别为r 1和r 2,则由S 1和S 2发出的光到达P点的波程差为δ=r 2-r 1。屏幕上的O点位于S 1和S 2连线的中垂线上,OP=x,则由图9.13可知,
时,两光束相互加强,该处为明条纹中心。式中,x的正、负表示干涉条纹是在O点两边对称分布的。对于O点,x=0,故δ=0,即k=0,因此O点为明条纹的中心,这个明条纹叫作中央明纹。在O点两侧,与k=1,2,…对应的x为
2λ,…,其波程差δ为±λ、±2λ,…,均为明纹中心,这些明条纹分别称为第一级、第二级……明条纹,它们对称地分布在中央明条纹两侧。
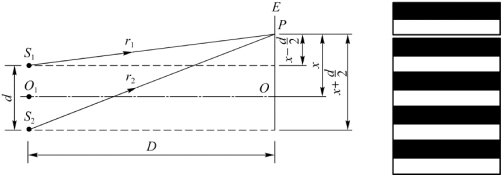
图9.13 干涉条纹的计算
当波程差δ满足
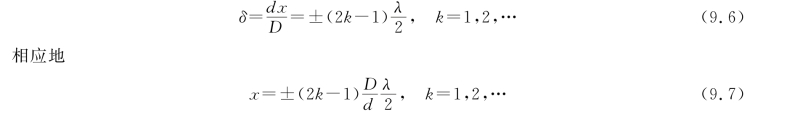
时,两光束相互减弱,该处为暗条纹中心。上式中k=1,2,…对应的暗条纹分别称为第一级、第二级……暗条纹。
由式(9.5)及式(9.7)可以计算出干涉图样中任何相邻的两条明条纹和任何相邻的两条暗条纹的间距都相等,即
式(9.8)表明,明条纹或暗条纹的间距与入射光波长及缝与屏幕的间距D成正比,与双缝间距d成反比,若d与D的值一定时,则条纹间距Δx只与入射光波长密切相关。波长较短的单色光的干涉条纹较密,波长较长的单色光的干涉条纹较疏。因此,若用白光照射双缝,则在屏幕上的干涉条纹是彩色的,中央为白色条纹,两侧对称地分布着由紫到红的各级干涉图谱。
例9.3 在杨氏双缝干涉实验中,假设相干光源S 1和S 2相距d=0.30 mm,S 1、S 2到屏幕E的垂直距离为D=2.0 m。
(1)若第二级明纹距中心点O的距离为6.0 mm,求此单色光的波长;
(2)求相邻两明条纹之间的距离。
解 (1)根据杨氏双缝干涉实验中明纹的位置公式(9.5),代入k=2,D=2.0 m,d=0.30 mm,r=6.0 mm,得
(2)根据相邻明纹间距公式(9.8)有
在杨氏双缝实验中,干涉区域是双缝后面的整个空间,另外,仅当缝S 1、S 2和S都很窄时,才能保证S 1和S 2处光波的振动有相同的位相,但这时通过狭缝的光太弱,因而干涉图样不够清晰。同时由于狭缝过窄,也有衍射现象发生,使得图样有些模糊。后来,许多科学家又尝试了一些其他的方法,对上述问题有所改善,其中较著名的有菲涅耳双面镜、双棱镜实验和洛埃镜实验等。这里我们只介绍洛埃镜实验。
洛埃镜实验不但能显示光的干涉现象,而且还能显示光由光疏介质(折射率较小的介质)射向光密介质(折射率较大的介质)而反射回来时的位相变化。图9.14所示为洛埃镜实验装置的示意图。洛埃镜实验中仅用一块平面镜KL即可产生光的干涉现象。由狭缝光源S 1发出的单色光一部分直接射到屏幕上,另一部分光以接近90°的入射角掠射到平面镜KL上,然后再由KL反射到屏幕上,S 2是S 1在平面镜KL中的虚像,S 2与S 1构成一对相干光源,但其中S 2为虚光源,由平面镜反射的光线好像是从S 2发出的。这样,当这两束光线在空间相遇时即可产生干涉现象,而在这两束光线叠加区域中放置的屏幕E上会看到明暗相间的等间距干涉条纹。
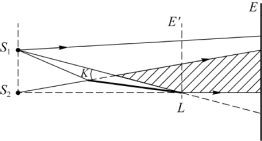
图9.14 洛埃镜实验装置简图
上述实验中,若把屏幕放到E′位置,这时屏幕与镜面L端刚好接触。在接触处,从S 1和S 2发出的光的路程相等,似乎在接触处应出现干涉明纹,但是实验事实指出,在屏幕和镜面的接触处为一暗纹。这表明,直接射到屏幕上的光与由镜面反射回来的光在镜与屏幕接触处位相相反,即位相差为π。由于入射光不可能有位相的变化,所以只能认为光从空气射向玻璃发生反射时,反射光有大小为π的位相突变。由波动理论可知,当位相差为π时,相当于光波行进中差了半个波长的距离,此即波动理论中的“半波损失”。因此,洛埃镜实验证明了光波由光疏介质入射到光密介质反射时会发生半波损失。