8.2 动生电动势
如式(8.1)所示,穿过一个闭合导体回路的磁通量发生变化时,回路中就产生感应电动势。但引起磁通量变化的原因可以不同,本节讨论导体在恒定磁场中运动时产生的感应电动势。这种感应电动势叫作动生电动势。
如图8.3所示,有一矩形导体回路,可动边是一根长为l的导体棒ab,它以恒定速度v在垂直于磁场B的平面内,沿垂直于它自身的方向向右平移,其余边不动。某时刻穿过回路所围面积的磁通量为
![]()
随着棒ab的运动,回路所围绕的面积扩大,因而回路中的磁通量发生变化。用式(8.1)计算回路中的感应电动势大小,可得
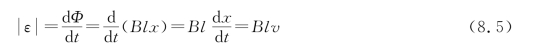
至于这一电动势的方向,可用楞次定律判定为逆时针方向。由于其他边都未动,所以动生电动势应归于ab棒的运动,因而只在棒内产生。回路中感生电动势的逆时针方向说明在ab棒中的动生电动势方向应沿由a到b的方向。像这样一段导体在磁场中运动时所产生的动生电动势的方向可以简便地用右手定则判断:伸直右手并使拇指与其他四指垂直,让磁感应线从掌心穿入,当拇指指着导体运动方向时,四指就指着导体中产生的动生电动势的方向。
像图8.3中所示的情况,感应电动势集中于回路的一段内,这一段可视为整个回路中的电源部分。由于在电源内电动势的方向是由低电势处指向高电势处,所以在棒ab上,b点电势高于a点电势。
我们知道,电动势是非静电力作用的表现。引起动生电动势的非静电力是洛伦兹力。当棒ab向右以速度v运动时,棒内的自由电子被带着以同一速度v向右运动,因而每个电子都受到洛伦兹力f的作用(图8.4),有
![]()
把这个作用力看成一种等效的“非静电场”的作用,则这一非静电场的强度应为
![]()
根据电动势的定义,又由于d r=d l为棒的长度元,棒ab中由该外来场所产生的电动势应为
![]()
如图8.4所示,由于v、B和d l相互垂直,所以式(8.8)的积分结果应为
εab=Blv
这一结果和式(8.5)相同。
图8.3 动生电动势
图8.4 动生电动势与洛伦兹力
这里我们只把式(8.8)应用于直导体棒在均匀磁场中运动的情况。对于非均匀磁场而且导体各段运动速度不同的情况,则可以先考虑一段以速度v运动的导体元d l,在其中产生的动生电动势为E ne·d l=(v×B)·d l,整个导体中产生的动生电动势应该是在各段导体之中产生的动生电动势之和。其表示式就是式(8.8)。因此,式(8.8)是在磁场中运动的导体内产生的动生电动势的一般公式。特别是,如果整个导体回路L都是在磁场中运动,则在回路中产生的总的动生电动势应为

在图8.3所示的闭合导体回路中,当由于导体棒的运动而产生电动势时,在回路中就会有感应电流产生。电流运动时,感应电动势是要做功的,电动势做功的能量是从哪里来的呢?考察导体棒运动时所受的力就可以给出答案。设电路中感应电流为I,则感应电动势做功的功率为
![]()
通有电流的导体棒在磁场中是要受到磁力的作用的。ab棒所受的磁力为F m=Il B,方向向左(图8.5)。为了使导体棒匀速向右运动,必须有外力F ext与F m平衡,因而F ext=-F m。此外力的功率为
![]() (https://www.daowen.com)
(https://www.daowen.com)
这正好等于上面求得的感应电动势做功的功率。由此我们知道,电路中感应电动势提供的电能是由外力做功所消耗的机械能转换而来的,这就是发电机内的能量转换过程。
我们知道,当导线在磁场中运动时产生的感应电动势是洛伦兹力作用的结果。根据式(8.10),感应电动势是要做功的。但是,我们早已知道洛伦兹力对运动电荷不做功,这个矛盾如何解释呢?可以这样来解释,如图8.6所示,随同导线一起运动的自由电子受到的洛伦兹力由式(8.6)给出,由于这个力的作用,电子将以速度v′沿导线运动,而速度v′的存在使电子还要受到一个垂直于导线的洛伦兹力f′的作用,f′=e v′×B。电子受洛伦兹力的合力为F=f+f′,电子运动的合速度为V=v+v′,所以洛伦兹力合力做功的功率为
![]()
这一结果表示洛伦兹力合力做功为零,这与我们所知的洛伦兹力不做功的结论一致。从上述结果中看到
![]()
即
f·v′=-f′·v
为了使自由电子按v的方向匀速运动,必须有外力f ext作用在电子上,而且f ext=-f′。因此式(8.13)又可写成
![]()
此等式左侧是洛伦兹力的一个分力使电荷沿导线运动所做的功,宏观上就是感应电动势驱动电流的功。等式右侧是在同一时间内外力反抗洛伦兹力的另一个分力做的功,宏观上就是外力拉动导线做的功。洛伦兹力做功为零,实质上表示了能量的转换与守恒。洛伦兹力在这里起了一个能量转换者的作用,一方面接受外力的功,同时驱动电荷运动做功。
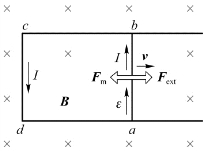
图8.5 能量转换
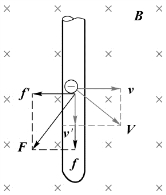
图8.6 洛伦兹力不做功
例8.1 法拉第曾利用图8.7所示的实验装置来演示感应电动势的产生。铜盘在磁场中转动时能在连接电流计的回路中产生感应电流。为了计算方便,我们设想一半径为R的铜盘在均匀磁场B中转动,角速度为ω(图8.8)。求盘上沿半径方向产生的感应电动势。
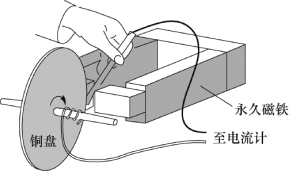
图8.7 法拉第电机
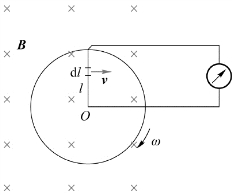
图8.8 铜盘在均匀磁场中转动
解 盘上沿半径方向产生的感应电动势可以认为是沿任意半径的一导体杆在磁场中运动的结果。由动生电动势公式(8.8),可求得在半径上长为d l的一段杆上产生的感应电动势为
dε=(v×B)·d l=Bv d l=Bωl d l
其中,l为d l段与盘心O的距离,v为d l段的线速度。整个杆上产生的电动势为
![]()
