3.1.2 质点的动量定理
设有一质量为m的质点,所受合力为F,将牛顿第二定律的导数形式
![]()
写成微分形式,即
![]()
式中,F d t为合力F的元冲量,d p为质点在d t时间内动量的变化。式(3.5)为质点动量定理的微分形式,可表述为:质点动量的微分等于作用在质点上合力的元冲量。因此,要使质点的动量发生变化,必须在冲量的作用下才有可能,仅有力的作用是不够的,力还必须累积作用一定时间。
对于在合力F作用下沿曲线运动的质点m,设质点在t 1时刻速度为v 1,在t 2时刻速度为v 2,将质点动量定理的微分形式积分可得
![]()
式(3.6)表明,质点所受合外力在某段时间内的冲量等于该质点在这段时间内动量的增量。这就是质点动量定理的积分形式。
只要外力的冲量一样,就会产生同样的动量增量。因此,要产生同样的动量增量,力大或者力小都可以。力大,需要的时间短些;力小,需要持续的时间长些。
动量定理是矢量方程,在直角坐标系中的分量式为
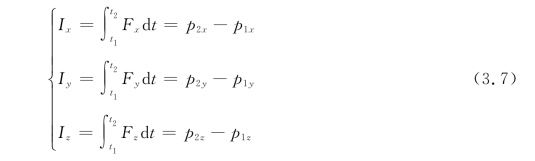
式(3.7)表明,质点在某方向受到冲量,该方向上的动量就会改变。
在碰撞、冲击等问题中,力的作用时间极短,但相互作用力很大且随时间急速变化,这种力通常叫作冲力。例如,球拍反击乒乓球的力、两汽车相撞时的力都是冲力。为了估算冲力的大小,常常需引入平均冲力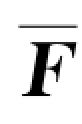 。
。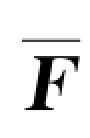 是冲力在碰撞时间内的平均值,在冲力作用时间内,平均冲力的冲量等于变化冲力的冲量,即
是冲力在碰撞时间内的平均值,在冲力作用时间内,平均冲力的冲量等于变化冲力的冲量,即
![]()
因此,平均冲力为

如图3.1所示,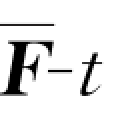 曲线下的面积与F-t曲线下的面积相等。
曲线下的面积与F-t曲线下的面积相等。
例3.1 如图3.2所示,质量为m的物体,由水平面上的点O以初速为v 0抛出,v 0与水平面成仰角α。若不计空气阻力,求:
(1)物体从发射点O到最高点的过程中重力的冲量;
(2)物体从发射点到落回至同一水平面的过程中重力的冲量。
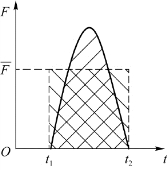
图3.1 方向恒定的变力的冲量
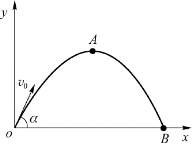
图3.2 例3.1用图
分析:重力是恒力,因此求其在一段时间内的冲量时,只需求出时间间隔即可。由抛体运动规律可知,物体到达最高点的时间![]() ,物体从出发到落回至同一水平面所需的时间是到达最高点时间的2倍。这样,按冲量的定义即可求出结果。
,物体从出发到落回至同一水平面所需的时间是到达最高点时间的2倍。这样,按冲量的定义即可求出结果。
另一种解的方法是根据过程的始、末动量,由动量定理求出。(https://www.daowen.com)
解 解法一:物体从出发到到达最高点所需的时间为
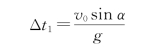
则物体落回地面的时间为
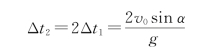
于是,在相应的过程中重力的冲量分别为
I A=-mgΔt 1j=-mv 0 sinαj
I B=-mgΔt 2j=-2mv 0 sinαj
解法二:根据动量定理,物体由发射点O运动到A、B的过程中,重力的冲量分别为
I A=mv Ay j-mv Oy j=-mv 0 sinαj
I B=mv By j-mv Oy j=-2mv 0 sinαj
例3.2 如图3.3所示,一质量为0.05 kg、速率为10 m/s的钢球以与钢板法线呈45°角的方向撞击在钢板上,并以相同的速率和角度弹回来。设碰撞时间为0.01 s。求在此时间内钢板所受到的平均冲力。
解 取钢球为研究对象,建立图3.3所示的坐标系。由动量定理得

例3.3 一辆装煤车以v=3 m/s的速率从煤斗下面通过,如图3.4所示,每秒落入车厢的煤为Δm=500 kg。如果使车厢的速率保持不变,应用多大的牵引力拉车厢?(车厢与钢轨间的摩擦忽略不计。)
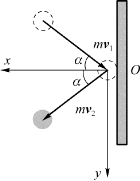
图3.3 例3.2用图
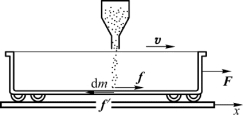
图3.4 例3.3用图
解 先考虑煤落入车厢后运动状态的改变。用d m表示在d t时间内落入车厢的煤的质量。它在车厢对它的力f的带动下在d t时间内沿x方向的速率由零增加到与车厢速率相同,而动量由零增加到v d m,由动量定理得,对d m在x方向应有
f d t=d p=v d m
对于车厢,在d t时间内,它受水平拉力F和煤d m对它的反作用力f′的作用。此二力的合力沿x方向,为F-f′。由于车厢速度不变,所以动量也不变,则有
(F-f′)d t=0
由牛顿第三定律可知,f′=f。所以
![]()
代入d m/d t=500 kg,v=3 m/s,可得
F=1.5×103 N
