3.2.2 动量守恒定律
由质点系动量定理知,在一过程中,若质点系所受合外力为零,则质点系的总动量不随时间改变。这就是质点系的动量守恒定律,即若
则
![]()

几点说明如下。
(1)动量定理及动量守恒定律只适用于惯性系。
(2)在牛顿力学中,因为力与惯性系的选择无关,故若在某一惯性系中动量守恒,则在其他任何惯性系中均守恒(这样的结论并非对所有守恒定律都适用,能否适用要看其守恒条件的成立是否不依赖于惯性系的选择)。
(3)若某个方向上合外力为零,则该方向上的分动量守恒,尽管总动量可能并不守恒。
(4)在一些实际问题中,当外力远小于内力且作用时间极短时(如两物体的碰撞),往往可以略去外力的冲量,而认为动量守恒。
(5)在牛顿力学的理论体系中,动量守恒定律是牛顿定律的推论。但动量守恒定律是比牛顿定律更普遍、更基本的定律,它在宏观和微观领域、低速和高速范围均适用。
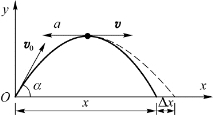
图3.7 例3.5用图
例3.5 质量为m′的人手里拿着一个质量为m的物体,此人用与水平面成α角的速率v 0向前跳去。当他达到最高点时,他将物体以相对于人为u的水平速率向后抛出。问:由于人抛出物体,他跳跃的距离增加了多少?(假设人可视为质点。)
解 取图3.7所示的坐标系。把人与物体视为一个系统,当人跳跃到最高点处向左抛物过程中,满足动量守恒,故有
(m+m′)v 0 cosα=m′v+m(v-u)
其中,v为人抛物后相对地面的水平速度,v-u为抛出物对地面的水平速度,得
![]() (https://www.daowen.com)
(https://www.daowen.com)
人的水平速度的增量为
![]()
而人从最高点到地面的运动时间为
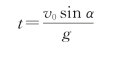
所以,人跳跃后增加的距离为
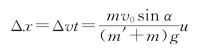
例3.6 如图3.8所示,设炮车以仰角θ发射一炮弹,炮车和炮弹的质量分别为M和m,炮弹的出口速度为v,求炮车的反冲速度V。炮车与地面间的摩擦力不计。
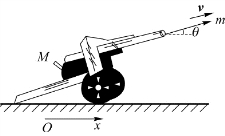
图3.8 例3.6用图
解 把炮车和炮弹看成一个系统。发炮前系统在竖直方向上的外力有重力和地面支持力,而在发射过程中重力与地面支持力虽反向但大小并不相等(想一想为什么),系统所受的外力矢量和不为零,所以这一系统的总动量不守恒。经分析,对地面参考系而言,炮弹相对地面的速度u,按速度变换,水平分量为
u x=v cosθ-V
于是,炮弹在水平方向的动量为m(v cosθ-V),而炮车在水平方向的动量为-MV。根据动量守恒定律有
-MV+m(v cosθ-V)=0
由此得炮车的反冲速度为
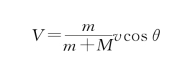
前面从表述宏观物体运动规律的牛顿运动定律出发导出了动量守恒定律。对可以用作用力与反作用力描述其相互作用的质点系所发生的过程,动量守恒定律成立;大量实验证明,对其内部的相互作用不能用力的概念描述的系统所发生的过程,如光子和电子的碰撞、光子转化为电子、电子转化为光子等过程,只要过程不受外界影响,它们的动量都是守恒的。动量守恒定律是关于自然界一切物理过程的基本守恒定律之一。
