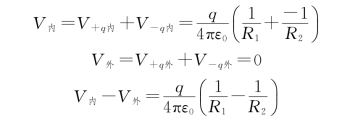5.5.4 电势的计算
计算电势的方法一般说来有两种:一种是根据电势的定义式通过对场强进行积分来计算;另一种是根据下面将要介绍的电势叠加原理来计算。
1.点电荷的电势
如图5.23所示,一个点电荷q处于O点处。在q所产生的电场中,距离O点为r的P点的电势可以根据电势的定义式计算得到。选无限远处作为电势零点,积分路径沿OP方向由P点延伸到无限远。由于积分方向选取的与场强的方向相同,P点电势可以很容易地计算出来,即
图5.23 点电荷的电势
![]()
式(5.31)给出了点电荷电场中任意一点的电势大小,称作点电荷电势公式。视q的正负,电势V P可正可负。在正点电荷的电场中,各点电势均为正值,离电荷越远的点,电势越低,与r成反比。在负点电荷的电场中,各点的电势均为负,离电荷越远的点,电势越高,无限远处电势为零。容易看出,以点电荷为球心的任意球面上电势都是相等的,这些球面都是等势面。
2.点电荷系的电势
如图5.24所示,设有点电荷q 1,q 2,…,qn,多个点电荷构成的点电荷系的场强满足场强的叠加原理,即有
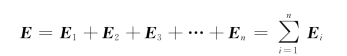
其中,E表示总电场,E 1,E 2,…,E n为单个点电荷产生的电场。根据电势的定义式,并应用场强叠加原理,电场中a点的电势可表示为
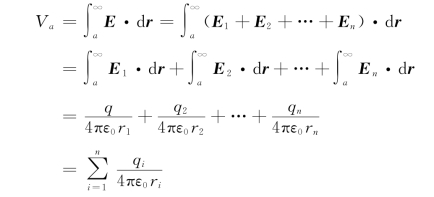
上式最后面一个等号右侧被求和的每一个积分分别为各个点电荷单独存在时a点的电势,即有

其中,V ai是第i个点电荷单独存在时在a点的电势。显然,如果我们将带电体系分成若干部分(不一定是点电荷),上述结论仍然是正确的。即任意一个电荷体系的电场中任意一点的电势等于带电体系各部分单独存在时在该点产生电势的代数和。这个结论叫作电势叠加原理。
3.连续带电体的电势
如图5.25所示,设连续带电体由无穷多个电荷元组成,每个电荷元可视为点电荷,取无限远处为零电势点,d q在a处产生的电势为
![]()
其中,r为电荷元d q到a点的距离。整个带电体在a处产生的电势为

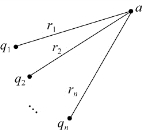
图5.24 点电荷系
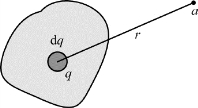
图5.25 电荷连续分布带电体
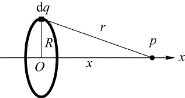
图5.26 例5.10用图(均匀带电圆环)
例5.10 均匀带电圆环半径为R,电荷为q,求其轴线上任意一点的电势。
解 如图5.26所示,x轴在圆环轴线上。
![]()
圆环在其轴线上任意一点产生的场强为
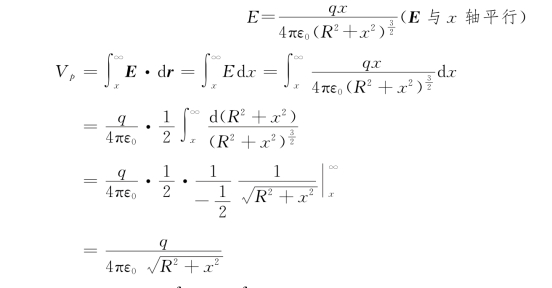 (https://www.daowen.com)
(https://www.daowen.com)
方法二:用电势叠加原理解![]()
把圆环分成一系列电荷元,将每个电荷元视为点电荷,d q在p点产生的电势为
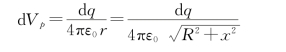
整个圆环在p点产生的电势为
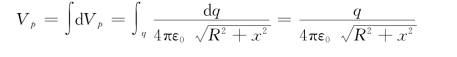
例5.11 一均匀带电球面半径为R,电荷为q,求球面外任一点的电势。
解 如图5.27所示取坐标系,场强分布为

球面外任一点P 1处的电势为
![]()
结论:均匀带电球面外任一点的电势,如同全部电荷都集中在球心的点电荷一样。
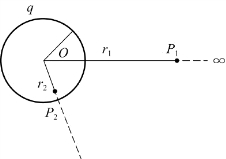
图5.27 例5.11用图(均匀带电球面电势)
球面内任一点P 2的电势为
![]()
可见,球面内任意一点的电势与球面上的电势相等。因为球面内任意一点的场强为零,所以在球面内移动试验电荷时,无电场力做功,即电势差为零,因而电势相等。
例5.12 有两个同心球面,半径分别为R 1、R 2,所带电荷为+q、-q,求两个球面的电势差。
解 方法一:用![]() 求解。
求解。
在两球面间,场强为
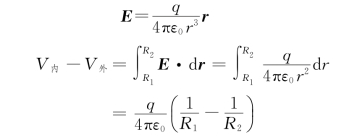
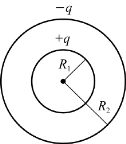
图5.28 例5.12用图(均匀带电同心球面)
方法二:用电势叠加原理求解。
内球面在两球面上产生的电势分别为
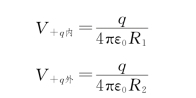
外球面在两球面上产生的电势分别为
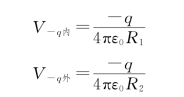
所以,根据叠加原理,两球面的电势分别为