2.5.2 非惯性系中牛顿第二定律的表达式
2026年01月14日
2.5.2 非惯性系中牛顿第二定律的表达式
一般来说,如果作用在物体上的力含有惯性力F i,那么牛顿第二定律的数学表达式为
![]()
或
F-(m a 0)=m a
式中,a 0是非惯性系相对于惯性系的加速度,a是物体相对于非惯性系的加速度,F是物体所受到的除惯性力以外的合外力。
例2.14 在图2.26所示的车厢内有一根质量可略去不计的细棒,其一端固定在车厢的
顶部,另一端系一小球,当列车以加速度a行驶时,细杆偏离竖直线α角,试求加速度a与摆角α之间的关系。
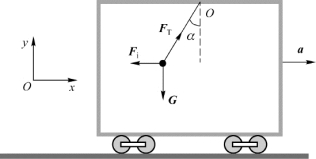
图2.26 例2.14用图(https://www.daowen.com)
解 设以加速度a运动的车厢为参考系,此参考系为非惯性系,在此非惯性系中的观测者认为,当细棒的摆角为α时,小球受到重力G、拉力F T和惯性力F i=-m a的作用。由于小球处于平衡状态,所以有
m g+F T=m a=0
上式在x轴和y轴上的分量式为
F T cosα-mg=0
F T sinα-ma=0
解得
a=g tanα
惯性力是在非惯性系中物体所受到的一种力,它是由于非惯性系本身的加速运动所引起的。惯性力不同于物体间相互作用所产生的力,它没有施力者,当然也不存在反作用力,从这个意义上可以说惯性力是“假想力”;然而在非惯性系中这个惯性力又是确实存在的,是可以感受和测量的,从这个意义上可以说惯性力是“真实力”。
事实上,在非惯性系中物体所受到的惯性力,从惯性系角度来看,完全是惯性的一种表现,因此,用“惯性力”来命名,正是考虑到了这一点。
