1.4 运动学中的两类问题
运动学的问题一般分为两大类。
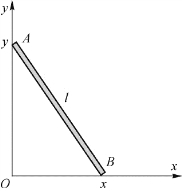
图1.29 例1.13用图
第一类问题是已知质点的位置矢量r=r(t),求质点的速度和加速度。这类问题可以通过对运动方程求时间的一阶导数得到速度,再求一次导数得到加速度,将具体的时间代入速度和加速度公式中就可以求得任意时刻的速度和加速度。
例1.13 如图1.29所示,长为l的细棒在竖直平面内沿墙角下滑,上端A匀速下滑,速度为v。当下端B离墙角距离为x(x<l)时,B端的水平速度和加速度各为多少?
解 建立如图1.29所示的坐标系。
设A端离地高度为y,则
x 2+y 2=l 2
方程两边对t求导
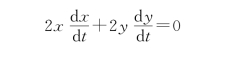
B端的水平速度为
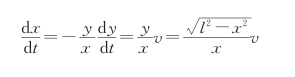
加速度为
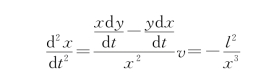
例1.14 质点做半径为R的圆周运动,其速率v=2t,求质点任意时刻的加速度a。
解 因为
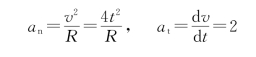
所以有
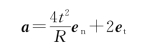
例1.15 已知一质点的运动方程为r=2t i+(2-t 2)j(SI),求:
(1)t=1 s和t=2 s时的位矢;
(2)t=1 s到t=2 s内的位移;
(3)t=1 s到t=2 s内质点的平均速度;
(4)t=1 s和t=2 s时质点的速度;
(5)t=1 s到t=2 s内的平均加速度;
(6)t=1 s和t=2 s时质点的加速度。
解 (1)r 1=(2i+j)m,r 2=(4i-2j)m
(2)Δr=r 2-r 1=(2i-3j)m
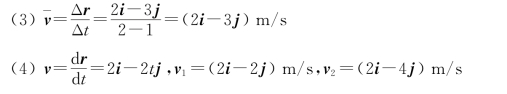
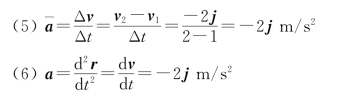
第二类问题是已知质点的加速度或速度,反过来求质点的速度、位置及运动方程。该类问题是通过对加速度或速度积分得到结果,积分常数要由问题给定的初始条件,如初始位置和初始速度来决定。
在加速度为已知的情况下,由a=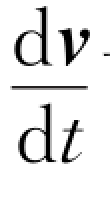 可得d v=a d t,把此式对过程积分可得到速度与加速度的积分关系
可得d v=a d t,把此式对过程积分可得到速度与加速度的积分关系

式中,v 0为t=0时质点的速度(初始条件中的初速度),它的分量形式为
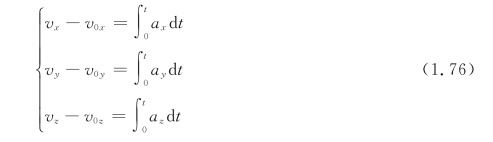
通过上面的积分运算后我们求得了速度,再由速度公式可得
![]()
式(1.77)表示,在Δt→0时,质点的位移d r等于速度v与时间间隔d t的乘积。这很像匀速运动,因为在极短的时间内,速度确实是可以看作不变的。把式(1.77)对过程积分,若初始条件为t=0时质点位矢为r 0,又设在任意t时质点位矢为r,则有积分
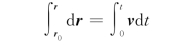
即

式(1.78)为位移与速度的积分关系,称为位移公式。用这个公式可由速度v来求位移Δr,进而通过初始位置r 0来求位矢r。同理可得到位移公式的三个分量式:

上述公式说明在已知加速度和初始条件的情况下求解速度和运动方程的一般方法。在直线运动中上述公式可以简化为

直线运动中,最简单的是匀速直线运动,质点的速度保持不变,加速度为零,即
v=常量, a=0
由于v=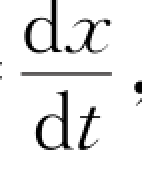 ,所以
,所以
d x=v d t
对此式两边积分,即可求出坐标x随时间的变化关系。设某一时刻的坐标为已知,例如t=0,坐标为x 0(称为初位置),则任一时刻t的坐标x就可由式(1.82)求出:

由于v=常量,所以由式(1.82)可得
![]()
这就是在匀速直线运动中,质点的坐标随时间变化的规律,也就是质点的运动方程。
在变速运动中,最简单的是匀变速直线运动。质点做这种运动时,加速度保持不变,即
![]()
同样,可以求
即
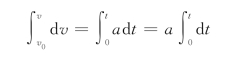
![]()
这是质点做匀变速直线运动时速度随时间变化的关系式。式中,v 0是t=0时刻质点的初速度。
又根据速度v=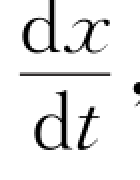 ,并设初位置t=0时x=x 0,则有
,并设初位置t=0时x=x 0,则有
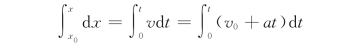
即
![]()
这就是匀变速直线运动的运动方程。
从式(1.84)和式(1.85)中消去t,就可得到速度随坐标变化的关系式
![]()
式(1.84)、式(1.85)、式(1.86)是读者在中学物理中所熟悉的。
在大学物理中常常会碰到更为复杂的情况,下面以直线运动为例进行讨论。
例1.16 一质点沿x轴运动,已知加速度为a=4t(SI),初始条件为:t=0时,v 0=0,x 0=10 m。求该质点的运动方程。
解 取质点为研究对象,由加速度定义有
![]()
可得
d v=4t d t
由初始条件有
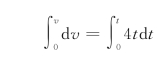
得
v=2t 2
由速度定义得
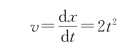
可得
d x=2t 2 d t
由初始条件得
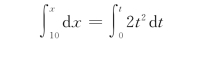
即
![]()
圆周运动角量的运动学问题完全类似于直线运动的情况。如果已知角运动方程求角速度和角加速度,就使用求导数的方法。如果已知角加速度和初始条件求角速度和角运动方程,则使用积分的方法。具体讲,由ω=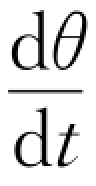 可得dθ=ωd t,把此式对过程积分,并设t=0时质点角位置在θ0,t时刻角位置在θ,则有角位移公式
可得dθ=ωd t,把此式对过程积分,并设t=0时质点角位置在θ0,t时刻角位置在θ,则有角位移公式

用同样的方法可由α=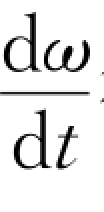 得 到角速度公式
得 到角速度公式

其中,ω0和ω分别为t=0时及t时刻的角速度。
当遇到角加速度与角速度有关或角加速度与角位置有关的情况时,积分的处理方法与前面的直线运动情况相类似。
例1.17 一质点沿圆周运动,其切向加速度与法向加速度的大小恒保持相等。设θ为质点在圆周上任意两点的速度v 1与v 2之间的夹角。试证:v 2=v 1 eθ。
证:因为
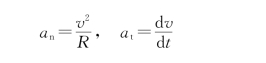
所以
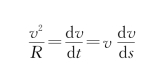
即
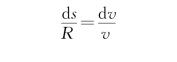
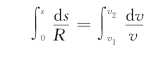
积分得
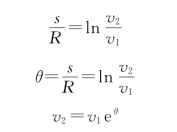
例1.18 如图1.30所示,飞机在高空点A时的水平速率为v A=1 940 km/h,沿近似于圆弧的曲线俯冲到点B,其速率为v B=2 192 km/h,所经历的时间为Δt=3 s。设圆弧AB的半径约为3.5 km,且飞机从A到B的俯冲过程可视为匀变速圆周运动。若不计重力加速度的影响,求:
(1)飞机在点B的加速度;
(2)飞机由点A到达点B所经历的路程。(https://www.daowen.com)
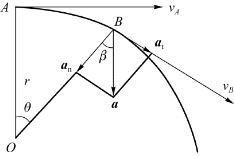
图1.30 例1.18用图
解 (1)由于飞机在A、B之间做匀变速圆周运动,所以d v/d t和角加速度α均为常量。切向加速度
a t的值为
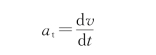
有
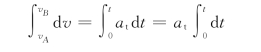
得点B的切向加速度为
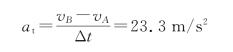
而在点B的法向加速度为
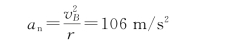
故飞机在点B时加速度的值为
![]()
a与a n之间的夹角β为
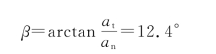
(2)在时间t内,径矢r转过的角度为
![]()
其中,ωA是飞机在点A的角速度。故在此时间内,飞机经过的路程为
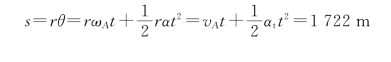
![]()
1.质点运动的描述(在笛卡儿坐标系中)
(1)位置和位移
·位置矢量为
r=x i+y j+z k
·r的大小为
![]()
·位矢r的方向可用方向余弦来表示:
![]()
·运动方程为
r=r(t)=x(t)i+y(t)j+z(t)k
·运动方程的分量形式为
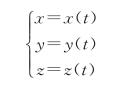
·位移为
Δr=r 2-r 1=Δx i+Δy j+Δz k
·位移的分量为
Δx=x 2-x 1,Δy=y 2-y 1,Δz=z 2-z 1
(2)速度
·平均速度为
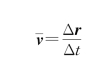
·平均速率为
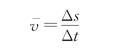
·速度为
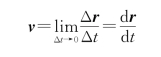
·速率为
![]()
·速度的分量为

(3)加速度
·平均加速度为
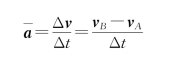
·加速度为
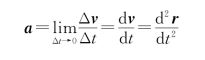
2.几种常见的运动
(1)一维直线运动
·质点运动方程为
x=x(t)
·位移为
Δx=x B-x A
·速度为
![]()
·加速度为
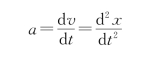
(2)平面运动
·质点运动方程为
r=x(t)i+y(t)j(矢量式),x=x(t),y=y(t)(分量式)
·速度为
v=v x i+v y j
·加速度
a=a x i+a y j
3.切向加速度和法向加速度
在自然坐标系中,以运动方向为正方向。
(1)运动方程为
s=s(t)
(2)速度为
![]()
(3)加速度为
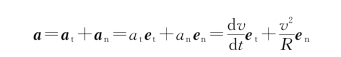
切向加速度为
![]()
法向加速度为

加速度的大小为
![]()
加速度与速度的夹角满足
![]()
v增加时a t>0,a t沿v的方向,θ为锐角;v减小时a t<0,a t逆v的方向,θ为钝角。
4.圆周运动的角量描述(在平面极坐标系中)
(1)角位置(角量运动方程)为
θ=θ(t)
(2)角速度为
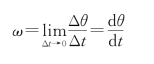
(3)角加速度为
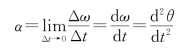
角速度公式为
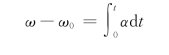
(4)角量与线量的关系
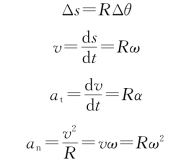
5.相对运动
(1)位置变换为
r=r 0+r′
(2)位移变换为
Δr=Δr′+ΔD
(3)速度变换为
ν=u+ν′
(4)加速度变换为
a=a′+a 0
