5.1.4 电场强度的计算
1.点电荷产生的电场
点电荷产生电场的规律可以通过库仑定律直接得到。如图5.2所示,一个静止的点电荷q在其周围产生电场,设场点P相对于q的位置矢量为r,简称矢径r。
现在假设有一个试验电荷q 0处于P点,根据库仑定律,试验电荷q 0所受的电场力为
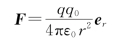
于是根据场强的定义我们可以得到

式(5.3)给出点电荷场中任意一点的场强的大小和方向,称作点电荷场强公式,从中可以看出点电荷产生电场的规律。r=r e r,r为P点的位置矢量,是从q指向P点的矢量。由式(5.3)可知,若q>0,则E与r同向,即在正电荷周围的电场中,任意一点的场强沿该点的矢径方向(图5.2(a));若q<0,则E与r反向,即在负电荷周围的电场中,任意点的场强沿该点矢径的负方向(图5.2(b))。式(5.3)还说明点电荷的电场具有球对称性,即在以q为球心的任意球面上场强大小相等,方向均与该球面正交。在各向同性的自由空间内,一个本身无任何方向特征的点电荷的电场分布必然具有这种对称性。
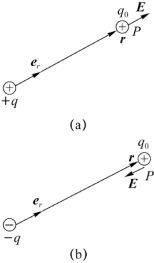
图5.2 点电荷的静电场
2.电场强度的叠加原理
一般来说,在某一个空间可能存在由许多个点电荷组成的点电荷系,为了能计算点电荷系的电场强度,下面我们先介绍电场强度的叠加原理。
如图5.3所示,试验电荷q 0放在点电荷系q 1,q 2,q 3,…,qn所产生的电场中的A点,实验表明q 0在A处受的电场力F是各个点电荷各自对q 0作用力F 1,F 2,F 3,…,F n的矢量和,即
![]()
按照场强定义有
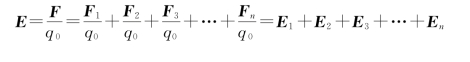

式(5.5)表明,点电荷系电场中任一点处的场强等于各个点电荷单独存在时在该点产生的场强的矢量和。
上述结论虽然是从点电荷系得出的,但显然容易推广到更一般的情况并得出如下普遍的结论:任意带电体系所激发的电场中某点的电场强度,等于该带电体系各个部分单独存在时在该点激发的电场强度的矢量和。这就是电场强度的叠加原理。
根据电场强度的叠加原理,点电荷系所产生的总电场的场强应等于各个点电荷场强的矢量和。对于包含n个点电荷的点电荷系,第i个点电荷q i在场点P产生的场强为
![]()
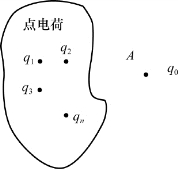
图5.3 点电荷系场强的叠加
式中,ri为场点P到点电荷q i的距离,e ri为P到q i矢径的单位矢量。按场强叠加原理,总场强为
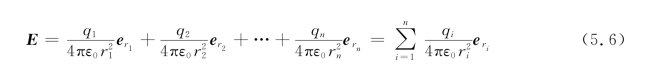
这就是点电荷系电场强度的计算公式。
3.连续带电体产生的电场
对于连续带电体所产生的电场,我们可以根据场强叠加原理和数学中的微积分方法计算。这种计算电场强度的方法叫作用叠加原理计算场强。
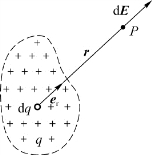
图5.4 连续带电体的电场计算
我们知道任何连续带电体都可以微分成点电荷d q,如图5.4所示。由前面所介绍的点电荷产生电场的规律,d q产生的场强为
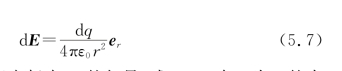
图5.4中r为d q指向场点P的矢量,式(5.7)中r为r的大小,e r为r的单位矢量。不同的元电荷指向P点的矢量r是不同的,因此r是一个变量。根据场强的叠加原理,带电体在P点处产生的总场强应该为各个元电荷在P点产生的场强的矢量和。这种无限多个无限小矢量的矢量和是一个矢量积分,即
![]()
根据带电体的几何特点,可以通过单位空间量度上分布的电荷电量——电荷密度求电荷元。
体电荷密度为

面电荷密度为

线电荷密度为
![]()
对应于连续带电体的体分布、面分布和线分布,可以写为如下三种形式:
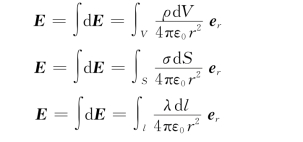
例5.1 电偶极子的静电场。
相距为l、带有等量异号电量的点电荷对构成一对电偶极子。
如图5.5所示,由-q指向+q的矢量l称为电偶极子的轴;p=q l,称为电偶极矩(简称电矩)。
![]()
图5.5 例5.1用图(一)
求:电矩p=q l的电偶极子在距中心r≫l处,
(1)轴线延长线上一点A处的电场强度;
(2)轴线中垂线上一点B处的电场强度。
解 (1)如图5.6(a)所示,建立坐标系,单位矢量e l=i。(https://www.daowen.com)
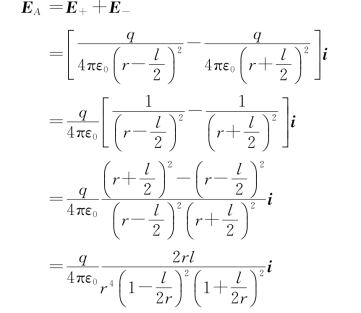
当r≫l时,
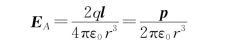
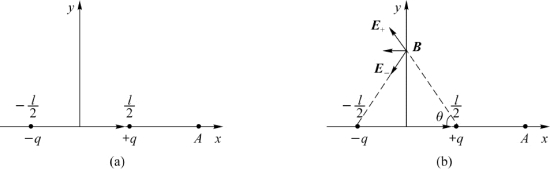
图5.6 例5.1用图(二)
(2)建立坐标系,如图5.6(b)所示。
两点电荷在B点产生的场强大小为
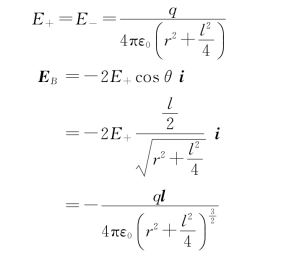
当r≫l时,
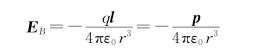
从以上计算结果可知,电偶极子产生的场强E的大小与电矩p成正比,与电偶极子到观察点的距离的三次方成反比。另外可证明,电偶极子在外电场中所受到的电场力、力矩都与电偶极子的电矩p成正比。因此,电矩p是电偶极子的一个重要特征量。
例5.2 有一均匀带电直线,长为l,电量为q,求距它r处p点的场强。
解 建立坐标系,如图5.7所示,把带电体分成一系列点电荷,d y段在p点处产生的场强为
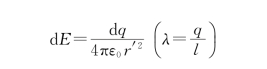
由图5.7可知
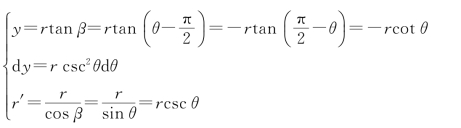
代入场强公式中有
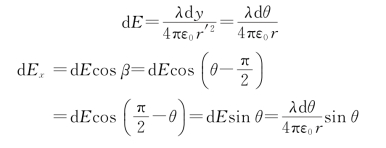
所以
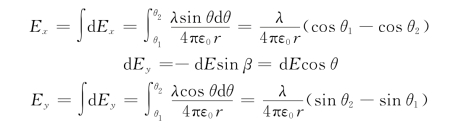
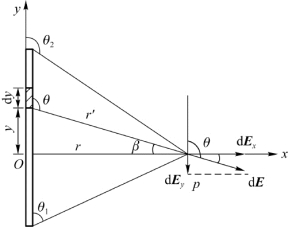
图5.7 例5.2用图(均匀带电直线的场强)
讨论:无限长均匀带电直线θ1=0,θ2=π,则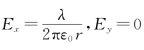 。即无限长均匀带电直线电场垂直于直线,λ>0,E背向直线;λ<0,E指向直线。
。即无限长均匀带电直线电场垂直于直线,λ>0,E背向直线;λ<0,E指向直线。
例5.3 设电荷q均匀分布在半径为R的圆环上,计算在环的轴线上与环心相距x的p点的场强。
解 建立坐标系,如图5.8所示,x轴在圆环轴线上,把圆环分成一系列长为d l的点电荷,d l部分在p点产生的电场为
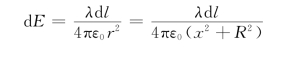
电荷线密度
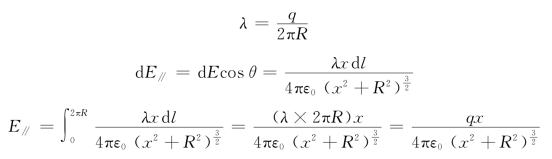
根据对称性可知,E⊥=0,因此
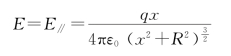
若q>0则E沿x轴正向;若q<0,则E沿x轴负向(x轴上E关于原点对称)。
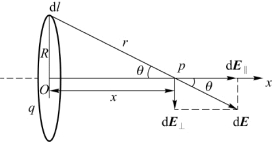
图5.8 例5.3用图(均匀带电圆环的场强)
结论:E与圆环平面垂直,环中心处E=0,也可用对称性判断。
当x≫R时,
![]()
例5.4 半径为R的均匀带电圆盘,电荷面密度为σ,计算轴线上与盘心相距x的p点的场强。
解 如图5.9所示,x轴在圆盘轴线上,把圆盘分成一系列的同心圆环,半径为r、宽度为d r的圆环在p点产生的场强为
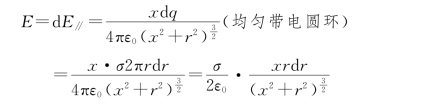
因为各环在p点产生的场强方向均相同,所以整个圆盘在p点产生的场强为
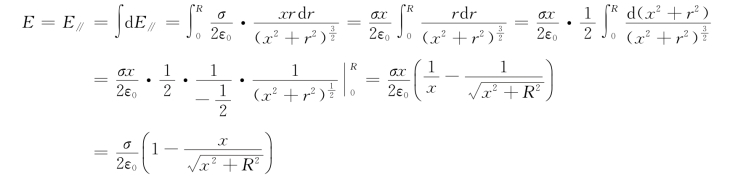
若σ>0,则场强背离圆盘;若σ<0,则场强指向圆盘。两种情况下E都与盘面垂直(E关于盘面对称)。当x≫R时,有E=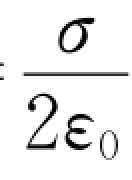 。
。
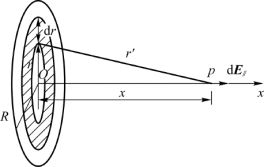
图5.9 例5.4用图(均匀带电圆盘的场强)
综合上面的例子,使用微积分计算场强的步骤如下:
①建立坐标系,目的是便于表示场强的方向和选择积分的变量;
②选取元电荷,即对连续带电体进行微分;
③写出元电荷在考察点的场强大小;
④分析元电荷在考察点场强的方向,为写分量做准备;
⑤写出元电荷在考察点场强的各个分量,为对各个分量积分做准备;
⑥分别对各个分量积分,并在积分过程中选择恰当的积分变量和统一变量。
