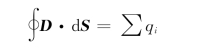6.5 电场能量
一个电中性的物体周围没有电场,当把电中性物体的正、负电荷分开时,外力做了功,这时该物体周围产生了电场。所以,通过外力做功可以把其他形式的能量转变为电能,储存在电场中。使一个系统带电,就是产生电场、储存电能的过程,如电容器的充电过程。使某个带电体放电,就是把电能转化为其他形式的能的过程,如电容器的放电过程。
以带电电容器为例进行讨论。给电容器充电的过程其实是电源将负极板上的正电荷搬运到正极板上,增大极板电量,提高极板电势差,建立电场的过程。
如图6.27所示,设t时刻,两极板上的电荷分别为+q(t)和-q(t),A、B间电势差为
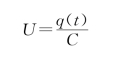
把电量d q从B移到A,外力做的功为
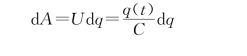
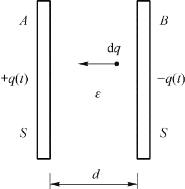
图6.27 电容器的能量
当A、B上电量达到+Q和-Q时,外力做的总功为
![]()
外力做的功全部转化为带电电容器储存的电能W e,所以电容器储存的电能为

对于平行板电容器,有
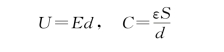
所以
![]()
其中,V=Sd,为电容器的体积。因为是匀强电场,W e应均匀分布,故单位体积内的能量即能量密度为

说明:
(1)式(6.13)适用于任何电容器;式(6.14)适用于任何电场。
(2)对任一带电系统整个电场能量为
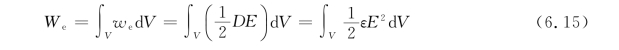
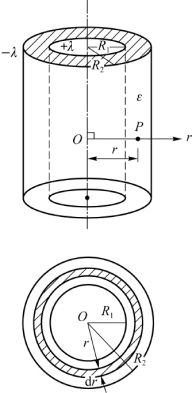
图6.28 例6.7用图
能量的存在是由于电荷的存在,电荷是能量的携带者,但式(6.15)表明,能量是存在于电场中的,电场是能量的携带者。在静电场中能量究竟是电荷携带的还是电场携带的,是无法判断的。因为在静电场中,电场和电荷是不可分割地联系在一起的,有电场必有电荷,有电荷必有电场,而且电场与电荷之间有一一对应关系,所以无法判断能量是属于电场还是属于电荷。但是,在电磁波情形下就不同了,电磁波是变化的电磁场的传播过程,变化的电场可以离开电荷而独立存在,没有电荷也可以有电场,而且场的能量能够以电磁波的形式传播,这一事实证实了能量是属于电场的,而不是属于电荷的。
例6.7 如图6.28所示,长为l的圆柱形电容器是由半径分别为R 1和R 2的两个同轴金属圆筒组成,两筒之间充满相对介电常数为εr的电介质。
(1)求电容器上的电场能量;
(2)证明:![]() ,Q、C分别为l长导体上的电量及l长电容器的电容。
,Q、C分别为l长导体上的电量及l长电容器的电容。
解 如图6.28所示取坐标系,原点在圆柱轴线且垂直于轴线为r轴。由题已知,其场是轴对称的,由高斯定理知,介质内任一点P的场强大小为(https://www.daowen.com)

(1)在半径为r、厚为d r、高为l的薄圆筒内,电场能量为
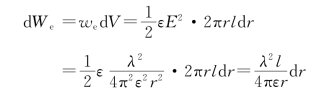
所求能量为
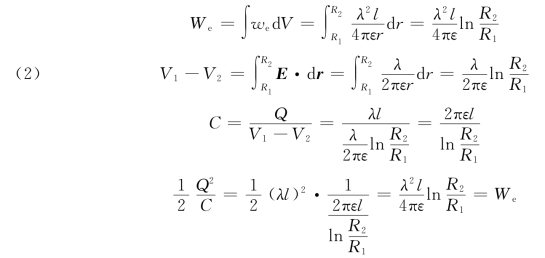
例6.8 如图6.29所示,有一个均匀带电荷为Q的球体,半径为R,试求电场能量。
解 由高斯定理知,场强为
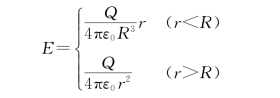
在半径为r、厚为d r的球壳内,能量为
![]()
图6.29 例6.8用图
所求能量为
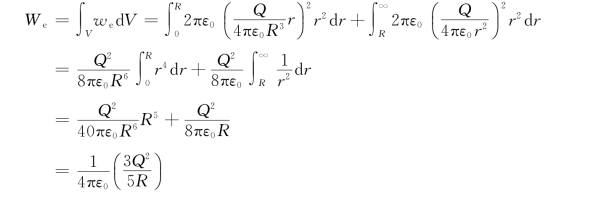
![]()
1.静电场中导体的性质
(1)导体的静电平衡条件:E in=0,表面外紧邻处E垂直于表面,导体是个等势体。
(2)计算有导体存在时的静电场分布问题的基本依据:电荷守恒、导体静电平衡条件、高斯定理、电势的概念。
(3)空腔导体的静电屏蔽:空腔导体(无论接地与否)将使腔内空间不受外电场的影响;而接地空腔导体将使外部空间不受空腔内电场的影响。
2.电容器
电容的定义:![]() ,C决定于电容器的结构;平行板电容器
,C决定于电容器的结构;平行板电容器![]() 。
。
3.电场能量密度、电容器的储能
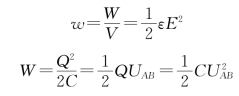
4.电介质对电场的影响
电介质在电场作用下发生电极化产生束缚电荷,从而削弱原来的电场。电容器间充满介质时
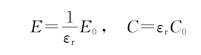
介质中的高斯定理: