2.5.3 离心力
下面介绍惯性离心力的概念。如图2.27所示,在水平放置的转台上,有轻弹簧系在细绳中间,细绳的一端系在转台中心,另一端系一质量为m的小球,设转台平面非常光滑,它与小球和弹簧的摩擦力均可略去不计。转台可绕垂直于转台中心的竖直轴以匀角速度ω转动。有两个观察者,一个站在地面上(处在惯性系中),另一个相对转台静止并随转台一起转动(处在非惯性中)。当转台转动时,站在地面上的观察者观察到弹簧被拉长。这时,绳对小球的作用力为指向转台中心的向心力F。力F的大小为mlω2。从牛顿第二定律来说,这一点是很好理解的,在向心力作用下,小球做匀速率圆周运动。而相对转台静止的另一个观察者虽也观察到弹簧被拉长,有力F沿向心方向作用在小球上,但小球却相对转台静止不动,这就不好理解了,为什么有力作用在小球上,小球却静止不动呢?于是这个观察者认为,要使小球保持平衡的事实仍然遵守牛顿第二定律,就必须想象有一个与向心力方向相反、大小相等的力作用在小球上一样,这个力F i叫作惯性离心力。应当注意,向心力和惯性离心力都是作用在同一小球上的,它们不是作用力和反作用力,也就是说,它们不遵守牛顿第三定律。
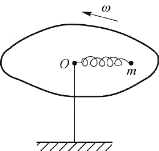
图2.27 离心力
例2.15 三棱柱以加速度a水平向左运动,它的斜面是光滑的,若质量为m的物体恰好能静止于斜面上,如图2.28(a)所示,求物体对三棱柱的压力。
解 解法一:若以地面为参考系,物体受到重力m g和支持力N的作用,如图2.28(b)所
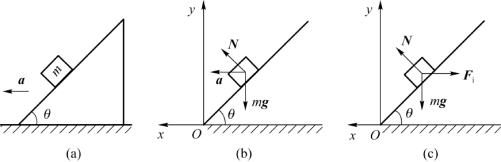
图2.28 例2.15用图
示。由牛顿第二定律得
N cosθ-mg=0
N sinθ=ma(https://www.daowen.com)
由以上两式得
![]()
解法二:若以三棱柱为参考系(非惯性系),那么物体除受重力m g和支承力N的作用外,还受惯性力F i的作用,如图2.28(c)所示。由牛顿第二定律得
N cosθ-mg=0
N sinθ-F i=0
其中
F i=ma
解上面两式可得与解法一一样的结果。
此例进一步说明,重力、压力、摩擦力等是真实的力,在惯性系和非惯性系中都存在,而惯性力则是虚拟的力,它只出现在非惯性系中。以下各章节若不特殊说明,仅讨论惯性系中物体的运动。
