1.2.3 圆周运动
1.自然坐标
在质点的平面曲线运动中,当运动轨迹已知时,常用自然坐标系表述质点的位置、路程、速度和加速度。例如,高速公路上奔驰的汽车,其轨迹是已知的。
如图1.15所示,在某质点运动的已知轨迹线上任选一固定点O点作为自然坐标原点,沿轨迹某一方向(如向右),量得质点所在位置P点与O点间轨迹的长度s来确定质点的位置。这样质点在轨迹上的位置就可以用s确定,这种确定质点位置的方法称为自然法,称s为质点的自然坐标。用自然坐标s表示的质点运动方程为
![]()
用自然坐标描述质点的平面曲线运动时,设t时刻质点处于P点,在P点取曲线的切线方向和法线方向,作相互垂直的两个坐标轴,一个轴沿轨道切向指向质点前进方向,其单位矢量用e n表示;另一轴沿轨道法向指向轨道凹侧,其单位矢量用e t表示。由于切向和法向坐标轴随质点沿轨道的运动自然变换位置和方向,通常称这种坐标系为自然坐标系。因此,一般来说,e n和e t不是恒矢量。
如图1.16所示,设质点t时刻在P点,自然坐标为s(t),t+Δt时刻在Q点,自然坐标为s(t+Δt)。在Δt时间内质点的位移为Δr,当质点经过Δt从P点到达Q点时,Δt内质点运动的路程为
![]()
当质点沿平面曲线运动时,其速度矢量的大小(速率)可以写为
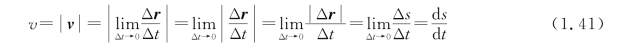
考虑其速度方向为轨道的切向,则速度矢量可表示为

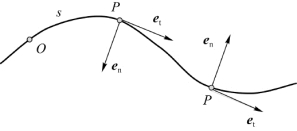
图1.15 自然坐标
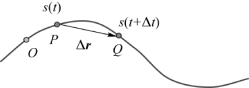
图1.16 自然坐标系中的路程与位移
2.匀速率圆周运动中的加速度
匀速圆周运动的特点是质点在运动过程中速率保持不变,但速度的方向是在不断变化的(因为是圆周运动)。在加速度的定义中我们知道,速度方向的变化也会有加速度。由于质点在固定的圆周上运动,速度方向变化的快慢显然与速率的大小有关。因此,在匀速圆周运动中质点的加速度也是与速率相关的。下面详细地讨论加速度的大小和方向。
如图1.17所示,质点从A点运动到B点有速度增量Δv存在。根据加速度的定义可得
![]()
显然,加速度a的方向与当Δt→0时Δv的极限方向一致。在速度增量的三角形图示中,当Δt→0即A点无限靠近B点时,Δθ的极限为零,则Δv的极限方向为垂直于v A且指向凹的一侧,即沿半径指向圆心,为该点加速度的方向。在大学物理中我们将它称为法向加速度,中学物理中将它叫作向心加速度。利用明显的相似三角形关系,我们有
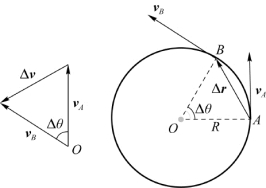
图1.17 匀速圆周运动的加速度
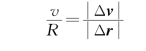
于是加速度的大小为

使用矢量可以同时将匀速圆周运动中法向加速度的大小和方向表示为
![]()
式中,e n表示轨迹法向的单位矢量。法向加速度在速度方向没有分量,它不改变速度的大小,只改变速度的方向。
3.变速圆周运动中的加速度
在变速圆周运动中,速度的大小和方向都在变化。如图1.18(a)所示,设质点t时刻在A点,速度为v A;t+Δt时刻质点在B点,速度为v B。Δr为过程中质点的位移,Δv为速度的增量,且Δv=v B-v A。
速度增量的矢量图如图1.18(b)所示,我们把Δv分解为两个分矢量,即
Δv=Δv n+Δv t(1.45)
其中,Δv n与初速度v A构成一个等腰三角形,而Δv t则沿着末速度v B所在直线。这两个分矢量的含义不同:Δv n描述速度方向的改变,Δv t描述速度大小的改变。把式(1.45)两边同时除以过程的时间间隔Δt,并令Δt→0,有
![]()
记作
![]()
式(1.47)左边为质点在t时刻的(总)加速度,右边第一项
![]()
称为法向加速度,第二项

称为切向加速度,它们的大小和方向将在下面分析。式(1.47)的含意是:质点的加速度为法向加速度和切向加速度的矢量和。
下面我们先分析法向加速度a n,这个分析与匀速圆周运动中讨论向心加速度的过程完全相同。于是我们得到质点法向加速度的大小为
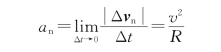
法向加速度的方向按式(1.48)应为当Δt→0时Δv n的极限方向,它显然是与速度v A垂直,即指向圆心的。
下面分析切向加速度a t。从图1.18(b)中可以看到,Δv的分量Δv t的大小等于速率的增量,记作
![]()
把此式两边同除以Δt并令Δt→0有
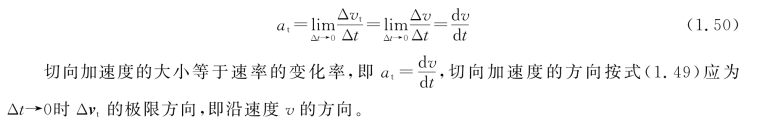
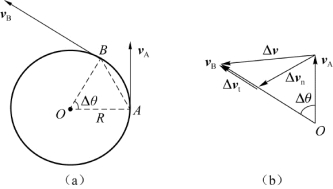
图1.18 变速圆周运动的加速度
以上结论是按质点的速率增加得到的。若质点的速率减小,则速度增量的分解应如图1.19所示。此时若令Δt→0,则Δv t的极限方向应与速度v的方向相反,即切向加速度将逆着速度v的方向。
综合以上两种情况,我们可以把切向加速度用一个带符号的量值(标量)来表示,其值为
![]()
当质点速率增加时,a t>0,表示切向加速度a t沿速度v的方向;当质点速率减小时,a t<0,表示切向加速度逆着速度的方向。
把质点的加速度分解为切向加速度和法向加速度是自然坐标描述的主要特点,这样做的好处是两个分量的物理意义十分清晰:切向加速度a t是由于速度数值的变化而引起的,描述质点速度大小变化的快慢;而法向加速度a n则是由速度方向的变化而引起,描述质点速度方向变化的快慢。沿切向和法向来分解加速度仍属于正交分解,如图1.20所示。
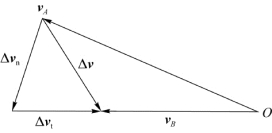
图1.19 减速圆周运动的加速度
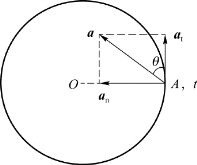
图1.20 圆周运动的加速度
可将质点做变速圆周运动时加速度的表达式(1.47)写成
![]()
在变速圆周运动中,由于速度的方向和大小都在变化,所以加速度a的方向不再指向圆心(图1.20),其值为
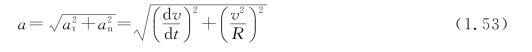 (https://www.daowen.com)
(https://www.daowen.com)
a与e t的夹角(图1.20)满足

其中,a n是法向加速度的大小,而a t为切向加速度的数值。若质点的速率在增加,a t>0,即a t沿速度v的方向,如图1.20中A点的情况,此时tanθ>0,即θ为锐角。若质点速率在减小,a t<0,即a t与v反向,此时tanθ<0,θ为钝角。但无论速率是增加还是减小,从图1.20中可以看到,由于法向加速度a n总是指向圆心(轨迹曲线的法向),所以加速度总是指向轨道凹的一侧。
4.圆周运动的角量描述
对圆周运动而言,由于圆周的半径是确定的,质点的位置可以使用与参考位置的角度来确定。这种方法叫作圆周运动的角量描述。
圆周运动的角量描述是一种简化的平面极坐标表示方法。
平面极坐标系的构成如图1.21所示,以平面上O点为原点(极点),Ox轴为极轴,建立一个平面极坐标系。平面上任一点p的位置,可用p到O的距离(极径)r和r与x轴的夹角(极角)θ来表示。
平面极坐标系适用于描述质点的圆周运动。以圆心为极点,沿一半径方向作一极轴Ox,则质点到O点的距离r即为圆半径R,是一个常量,故质点位置仅用夹角θ即可确定。θ称为质点的角位置,它实际上只代表质点相对于原点的方向。θ随时间t变化的关系式为
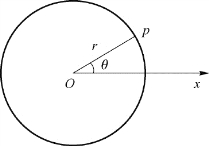
图1.21 平面极坐标
![]()
称为角量运动方程。质点在从t到t+Δt过程中角位置的变化叫作角位移。
![]()
通常取逆时针转向的角位移为正值。
质点在做圆周运动时,在一段时间内的角位移与时间间隔的比值定义为角速度。在有限长时间段内的角位移与时间间隔的比值叫作平均角速度,即
![]()
而在无限短时间内角位移与时间间隔的比值叫作瞬时角速度,简称为角速度。根据极限的概念,在Δt→0时平均角速度的极限就是质点在t时刻的瞬时角速度,即
![]()
即角速度为角位置的时间变化率(角位置对时间的一阶导数),通常以逆时针转动的角速度为正。角速度的单位是rad/s。
圆周运动过程中角速度增量与时间间隔的比值定义为角加速度,常用α表示。所谓角速度增量是指质点在t到t+Δt过程中末角速度与初角速度之差,即
![]()
在有限长的时间段内角速度增量与其时间间隔Δt之比称为平均角加速度,即
![]()
在无限短的时间间隔内角速度增量与其时间间隔之比称为瞬时角加速度,简称角加速度。同样根据极限的概念,在Δt→0时平均角加速度的极限即为质点在t时刻的瞬时角加速度,即
![]()
即角加速度为角速度对时间的变化率(即角速度对时间的一阶导数,或角运动方程对时间的二阶导数)。角加速度的单位是rad/s2。
5.圆周运动中角量与线量的关系
质点的圆周运动常用平面极坐标系和自然坐标系描述。极坐标是用角位移、角速度和角加速度等物理量来描述圆周运动,称为角量描述,而自然坐标是用路程、速率、切向加速度及法向加速度来描述圆周运动,称为线量描述。两种描述之间的关系比较简单,如图1.22所示。设质点沿半径为R的圆周运动,以p点为路程起点,以运动方向为正方向,也就是角位置θ和路程s增加的方向。设质点t时刻在p 1点,其角位置为θ,路程为s,则有
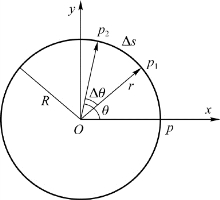
图1.22 角量和线量的关系
![]()
若t+Δt时刻质点到p 2点,过程中质点路程为Δs,角位移为Δθ,则角位移与路程的关系为
![]()
将式(1.62)对时间t求导得到质点速率
![]()
再将式(1.64)对时间t求导得质点的切向加速度
![]()
而质点的法向加速度为

有时质点在圆周上运动的方向是变化的,此时式(1.62)和式(1.64)中的θ和ω可能为负值,则s和v也为负值,可把s看作弧坐标,v看作速度,均设为标量。若s、v及a t为负,则表示它们与所设的正方向反向。
例1.9 在一个转动的齿轮上,一个齿尖P沿半径为R的圆周运动,其路程s随时间的变化规律为s=v 0t+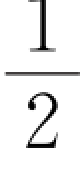 bt 2,其中,v 0、b都是正的常数,则t时刻齿尖P的速度和加速度大小为多少?
bt 2,其中,v 0、b都是正的常数,则t时刻齿尖P的速度和加速度大小为多少?
解
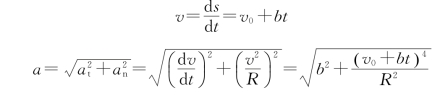
6.曲线运动中的法向与切向加速度
一般曲线运动的轨道不是一个圆周,但轨道上任何一点附近的一段极小的线元都可以看作某个圆的一段圆弧,这个圆叫作轨道在该点的曲率圆,如图1.23所示,其中心叫作曲率中心,半径叫作曲率半径ρ。当质点运动到这一点时,其运动可以看作在曲率圆上进行的,所以前述对圆周运动法向和切向加速度的讨论及结论此时仍能适用,如图1.24所示。不同的是,在一般曲线运动中法向加速度的大小a n=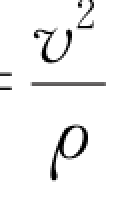 ,其中的ρ应是考察点的曲率半径,法向加速度的方向应指向考察点的曲率中心。圆周运动是一种特殊的曲线运动,对圆周上的任一点,只有一个曲率圆即圆周自身,而一般曲线运动在轨迹的不同点有不同的曲率圆(图1.23)。
,其中的ρ应是考察点的曲率半径,法向加速度的方向应指向考察点的曲率中心。圆周运动是一种特殊的曲线运动,对圆周上的任一点,只有一个曲率圆即圆周自身,而一般曲线运动在轨迹的不同点有不同的曲率圆(图1.23)。
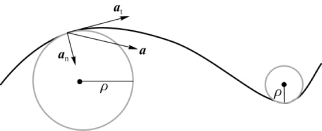
图1.23 轨道的曲率圆
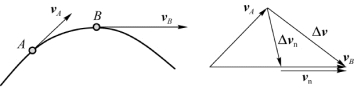
图1.24 一般曲线运动的加速度
一般曲线运动中的法向加速度和切向加速度的大小分别为

例1.10 一物体做抛体运动,当速率v=20 m/s时,速度的方向与水平方向成θ=30°仰角(重力加速度g=9.8 m/s2),求:此时物体的
(1)切向加速度;
(2)法向加速度;
(3)曲率半径。
解 物体在运动中,总加速度为重力加速度g,如图1.25所示。
(1)切向加速度的大小为
a t=-g sinθ=-9.8sin 30°=-4.9 m/s2
(2)法向加速度的大小为
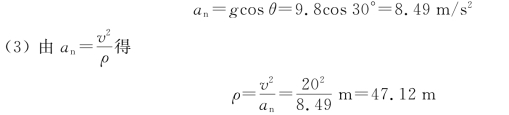
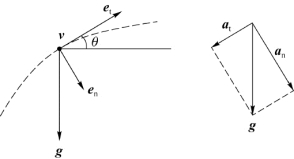
图1.25 例1.10用图
