9.1.1 光线的反射与折射
几何光学是以下列几个实验定律为基础建立起来的,它是各种光学仪器设计的理论根据。
光的直线传播定律:光在均匀介质里沿直线传播。光能够在其中传播的物质称为光介质,简称介质。
在点光源的照射下,不透明的物体背后出现清晰的影子。影子的形状与以光源为中心发出的直线所构成的几何投影形状一致(图9.1)。如果在一个暗箱的前壁上开一个小孔,由物体上各点发出的光线将沿直线通过小孔,在暗箱的后壁上形成一倒立的像(图9.2)。以上两个例子都表明光线沿直线传播的基本事实。
图9.1 影子
图9.2 针孔成像
应当注意,光线只在均匀介质中沿直线传播。当光从一种介质进入另一种不同介质时,光的传播方向发生变化,这种现象称为光的折射。在非均匀介质中光线将因折射而弯曲,这种现象经常发生在大气中。例如,在海边有时出现的海市蜃楼幻境便是由光线在密度不均匀的大气中折射引起的。
在研究光的传播过程时,可以用一条表示光束的直线来代表这束光,这样的直线就称为光线。在画图的时候,经常用带箭头的线段来表示沿箭头所指方向传播的光线。
设介质1、2都是透明、均匀和各相同性的,且它们的分界面是平面(如果分界面不是平面,但曲率不是太大,则以下结论仍然适用)。当一束光线由介质1入射到分界面上时,在一般情况下它将分解为两束光线:反射光线和折射光线(图9.3)。入射光线与分界面的法线构成的平面称为入射面,分界面法线与入射光线、反射光线和折射光线所成的夹角i 1、i′1、i 2分别称为入射角、反射角和折射角。实验表明:
(1)反射光线与折射光线都在入射面内;
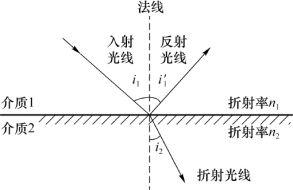
图9.3 光的反射和折射
(2)反射角等于入射角,即
![]()
(3)入射角与折射角的正弦之比与入射角无关,是一个与介质和光的波长有关的常数,即
![]()
比例常数n 12称为第二种介质相对于第一种介质的折射率。式(9.2)有时称作斯涅尔定律。
任何介质相对于真空的折射率称为该介质的绝对折射率,简称折射率,记作n,等于光在真空中的传播速度(c=3.0×108 m/s)与光在这种介质中的传播速度v的比值,即
![]()
式(9.1)又可写作

n 1、n 2分别为介质1和介质2的折射率。由于光在真空中的传播速度大于光在任何其他介质中的传播速度,所以折射率n总是大于1的。光从真空进入任何其他介质时入射角总是要大于折射角的。又因为光在真空中的速度与空气中的速度相差很小,可以认为光从空气进入某种介质的折射率就是那种介质的折射率。常见介质的折射率如表9.1所示。
表9.1 常见介质的折射率
 (https://www.daowen.com)
(https://www.daowen.com)
折射率反映了介质对光在折射方面的性质,由光在该介质中的传播速度决定。两种介质相比较,折射率大的称为光密介质,折射率小的称为光疏介质。光密介质与光疏介质是相对的,因此单说一种介质是光密介质还是光疏介质是没有意义的。不同介质折射率的大小与密度无关,同种介质密度增大时折射率也增大。
由于c是已知的,根据式(9.2),测出介质的折射率就可求出光在该介质中的传播速度。另外,由光的反射定律可知,如果光线逆着反射光线的方向入射到反射面上,则一定可以在原来入射光的角度上得到这束光的反射光。所以,反射现象也遵循光路可逆的规律。
日常生活中遇到的光的反射大多发生在粗糙、不光滑的表面上,即便是用平行光作为入射光,反射光也会指向许多不同的方向,这种反射称为漫反射,如图9.4所示。与之相反,平行入射的光线被某些非常光滑的反射面反射后,仍然保持平行,这种反射称为镜面反射,如图9.5所示。镜面反射和漫反射都遵循光的反射定律,在日常生活中,根据实际需要,要积极发挥它们的有利因素,克服它们造成的不利影响。
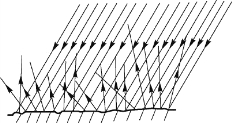
图9.4 漫反射
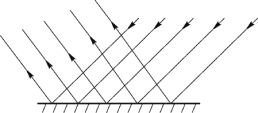
图9.5 镜面反射
例9.1 设有一束白光从玻璃射入空气中,玻璃的折射率为1.53,空气的折射率为1,当入射角为30°时,折射角为多少?
解 根据式(9.2)有
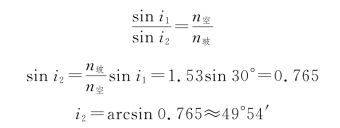
即折射角i 2约为49°54′。
由例9.1可知,当光从光密介质射入光疏介质时,入射角小于折射角。让光线逆着折射光线的方向射入光密介质时,则一定可以在原来入射光的角度上得到这束光的折射光,所以折射现象也遵循光路可逆的规律。同时,也可以证明光从光疏介质射入光密介质时,入射角大于折射角。
两个表面相互平行的平面透明体称为平行透明板。平板玻璃、玻璃砖等都是平行透明板。如图9.6所示,光通过玻璃砖时,光线方向并不发生改变,只是发生了侧移。
证明如下:
根据折射定律,在AB界面上
n 1 sin i 1=n 2 sinγ1
在A′B′界面上
n 2 sinγ2=n 1 sin i 2
因为AB∥A′B′,γ1=γ2,所以
sin i 1=sin i 2
i 1=i 2
即光线MO∥O′N。
可见,光通过两平行的透明板后并不改变方向,只是发生了侧向偏移。透明板越厚或入射角越大,光线偏向侧移就越大。
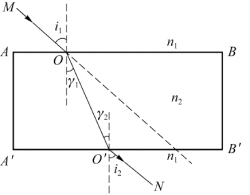
图9.6 光的侧移现象示意图
