8.6 麦克斯韦方程组
1.麦克斯韦方程组
电磁学的基本规律是真空中的电磁场规律,它们是这就是关于真空的麦克斯韦方程组的积分形式。在已知电荷和电流分布的情况下,这组方程可以给出电场和磁场的唯一分布。特别是当初始条件给定后,这组方程还能预言电磁场此后变化的情况。正像牛顿运动方程能完全描述质点的动力学过程一样,麦克斯韦方程组能完全描述电磁场的动力学过程。
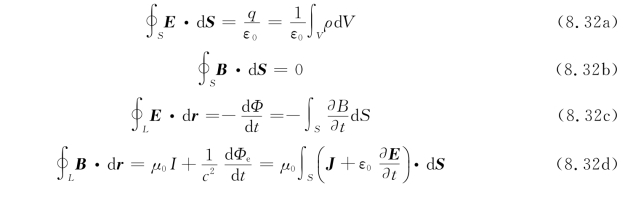
下面再简要地说明一下方程组(8.32)中各方程的物理意义。
·方程(8.32a)是电场的高斯定理,它说明电场强度和电荷的联系。尽管电场和磁场的变化也有联系(如感生电场),但总的电场和电荷的联系服从这一规律。
·方程(8.32b)是磁通连续性定理,它说明,目前的电磁场理论认为在自然界中没有单一的“磁荷”(或磁单极子)存在。
·方程(8.32c)是法拉第电磁感应定律,它说明变化的磁场和电场的联系。虽然电场和电荷也有联系,但总的电场和磁场的联系符合这一规律。
·方程(8.32d)是一般形式下的安培环路定理,它说明磁场和电流(即运动的电荷)以及变化的电场的联系。
为了求出电磁场对带电粒子的作用从而预言粒子的运动,还需要洛伦兹力公式,即
F=q E+q v×B
这一公式实际上是电场E和磁场B的定义。
2.磁单极子
在麦克斯韦电磁场理论中,就场源来说,电和磁是不相同的:有单独存在的正的或负的电荷,而无单独存在的“磁荷”——磁单极子,即无单独存在的N极或S极。根据“对称性”的想法,这似乎是“不合理的”,因此人们总有寻找磁荷的念头。1931年,英国物理学家狄拉克(P.A.M.Dirac,1902—1984年)首先从理论上探讨了磁单极子存在的可能性,指出磁单极子的存在与电动力学和量子力学没有矛盾。他指出,如果磁单极子存在,则单位磁荷g 0与电子电荷e应该有下述关系:
g 0=68.5e
由于g 0比e大,所以库仑定律将给出两个磁单极子之间的作用力要比电荷之间的作用力大得多。
在狄拉克之后,关于磁单极子的理论有了进一步的发展。1974年,荷兰物理学家特霍夫脱和苏联物理学家鲍尔亚科夫独立地提出的非阿贝尔规范场理论认为磁单极子必然存在,并指出它比已经发现的或是曾经预言的任何粒子的质量都要大得多。现在关于弱电相互作用和强电相互作用的统一的“大统一理论”也认为有磁单极子存在,并预言其质量为2×10-11 g,即约为质子质量的1016倍。
磁单极子在现代宇宙论中占有重要地位。有一种大爆炸理论认为超重的磁单极子只能在诞生宇宙的大爆炸发生后10-35 s产生,因为只有这时才有合适的温度(1030 K)。当时单独的N极和S极都已产生,其中一小部分后来结合在一起湮没掉了,大部分则留了下来。今天的宇宙中还有磁单极子存在,并且在相当于一个足球场地的面积上,一年约可能有一个磁单极子穿过。
以上都是理论的预言,与此同时也有人做实验试图发现磁单极子。例如,1951年,美国的密尔斯用通电螺线管来捕集宇宙射线中的磁单极子(图8.20)。如果磁单极子进入螺线管中,则会被磁场加速而在管下部的照相乳胶片上显示出它的轨迹。实验结果没有发现磁单极子。
有人利用磁单极子穿过线圈时引起的磁通量变化能产生感应电流这一规律来检测磁单极子。例如,在20世纪70年代初,美国埃尔维瑞斯等人试图利用超导线圈中的电流变化来确认磁单极子通过了线圈(图8.21)。他们想看看登月飞船取回的月岩样品中有无磁单极子,当月岩样品通过超导线圈时,并未发现线圈中电流有什么变化,因而不曾发现磁单极子。
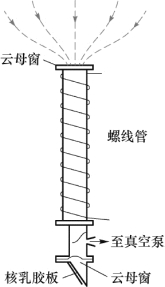
图8.20 磁单极子捕集器(https://www.daowen.com)
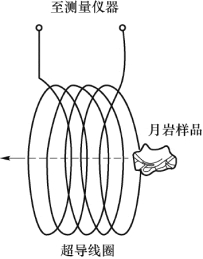
图8.21 检测月岩样品
1982年,美国卡勃莱拉也设计制造了一套超导线圈探测装置(图8.22),并用超导量子干涉仪(SQUID)来测量线圈内磁通的微小变化,他的测量是自动记录的。1982年2月14日,他发现记录仪上的电流有了突变。经过计算,正好等于狄拉克单位磁荷穿过线圈时所应该产生的突变。这是他连续等待了151天所得到的唯一的一个事例,以后虽扩大线圈面积也没有再测到第二个事例。
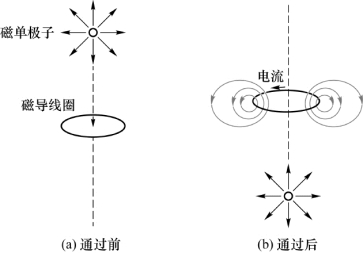
图8.22 磁单极子通过超导线圈时产生电流突变
还有其他的实验尝试,但直到目前还不能说在实验上确认了磁单极子的存在。
![]()
1.法拉第电磁感应定律
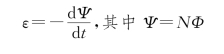
2.动生电动势
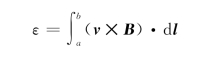
3.感生电动势
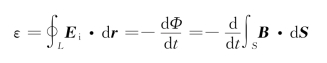
4.自感电动势
![]()
5.互感电动势
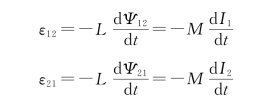
6.一般磁场的磁能
![]()
磁能密度
![]()
