3.3.1 质心
2026年01月14日
3.3.1 质心
设一个质点系由N个质点组成,以m 1,m 2,…,mi,…,m N分别表示各质点的质量,以r 1,r 2,…,ri,…,r N分别表示各质点对某一坐标原点的位矢,如图3.9所示。设质心C的位矢为r C,它的定义式如下:
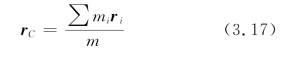
m是质点系的总质量,即r C是质点位矢以质量为权重的平均值。
![]()
质心位矢与坐标系的选择有关,但可以证明,质心相对于质点系各质点的相对位置是不会随坐标系的选择而变化的,即质心是相对于质点系本身一个特定位置的。
利用位矢沿直角坐标系各坐标轴的分量,可以得到质心坐标的分量式如下:
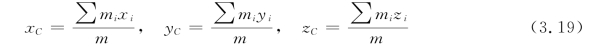
一个大的连续的物体可以认为是由许多质点(或称质元)组成的,以d m表示其中任一质元的质量,以r表示其位矢,则质量连续分布的大物体的质心位置可用积分法求得,即有

其在直角坐标系下的三个坐标分量式分别为
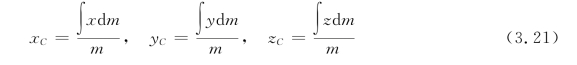
从上面的公式可以发现,均匀直棒、均匀圆环、均匀圆盘、均匀球体等物体的质心在它们的几何对称中心上。(https://www.daowen.com)
物体的重心与质心有区别。重心是物体各部分所受重力的合力作用点。对于小线度物体(其上各处重力加速度相等),质心和重心是重合的。
例3.7 将一均匀细铁丝弯成半径为R的半圆环,求其质心。
解 建立图3.10所示的直角坐标系。设铁丝的线密度为λ。根据对称性,质心在其对称轴y轴上,显然x C=0。
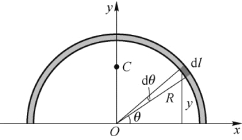
图3.10 例3.7用图
任一线元的质量为
d m=λd l, d l=R dθ
位置为
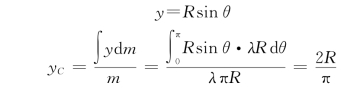
半径为R的半圆形均匀薄板的质心坐标为![]() 。
。
注意,半圆环形铁丝的质心并不在铁丝上,但它相对于铁丝的位置是确定的。
