5.2.2 电场强度通量
电场强度通量也叫电通量,是我们对静电场进行理论分析时所必需的一个重要物理量。为了能严格地定义电场强度通量,我们首先介绍有向曲面的概念。
通过电场中某一个曲面的电场线条数叫作通过这个面的电通量,用由Φe表示。下面我们分几种情况来说明计算电通量的方法。
1.均匀电场中,平面与场强E垂直
在场强为E的匀强电场中,与场强E垂直的平面面积为S⊥,如图5.12(a)所示。根据作电场线的规定,通过与场强垂直的单位面积上的电力线条数等于场强的大小,这样通过S⊥面的电通量为
Φe=ES⊥
2.均匀电场中,平面法线与场强夹角为θ
由图5.12(b)可见,通过平面S的电通量等于通过它在垂直于E的平面上的投影S⊥面的电通量,所以通过平面S的电通量为
![]()
式中,S=S e n,e n为S的单位法线向量。
图5.12 电通量
3.非均匀电场中的任意曲面
先把曲面S划分成无限多个面积元d S,如图5.12(c)所示,每个面积元都可看成无限小平面,它上面的场强可当作均匀的。设面积元d S的法线e n与该处场强E成θ角,则通过面积元d S的电通量为(https://www.daowen.com)
dΦe=E cosθd S
通过曲面S的电通量Φe应等于曲面上所有面积元的电通量dΦe的代数和,即
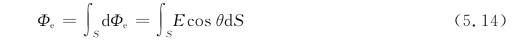
式中,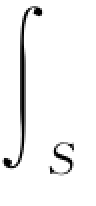 表示对整个曲面S进行积分。
表示对整个曲面S进行积分。
4.非均匀电场中的闭合曲面
通过闭合曲面的电通量为
![]()
若引入面积元矢量d S(大小等于d S而方向是d S的正法线e n方向),d S=d S e n,由矢量的标积定义可知,E cosθd S为矢量E和d S的标积,即有E cosθd S=E·d S,那么
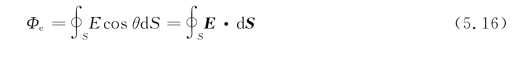
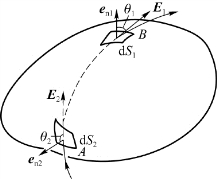
图5.13 闭合曲面的电通量
式中,∮S表示对整个闭合曲面进行积分。对于不闭合的曲面,面上各处法向单位矢量的正向可以任意取这一侧或另一侧。对于闭合曲面,通常规定面积元d S的法线方指向曲面外侧为正方向,这时通过闭合曲面上各面积元的电通量可正可负。如图5.13所示,在面积元A处,电力线从曲面外穿进曲面内,由于θ2>90°,所以电通量dΦe为负;在面积元B处电场线从曲面内穿出到曲面外,由于θ1<90°,所以电通量dΦe为正。因此,式(5.16)表示的通过整个闭合曲面的电通量,就等于穿入与穿出闭合曲面的电场线条数之差,即电通量就等于该闭合曲面的电场线的净穿出。
