4.1 功
恒力的功的定义为:力F在质点位移方向上的投影与位移大小|Δr|的乘积(即A=F cosθ|Δr|)是力对空间的积累效应,如图4.2所示,写成矢量式即
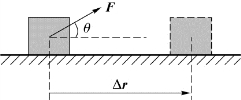
图4.2 恒力的功
![]()
那么变力的功如何计算呢?
当物体受一变力在空间中持续一个过程,如持续一段曲线,如图4.3所示,且F随空间变化,这时需要将物体经过的路径无限分割成很多微小的曲线段,每个微小曲线段上的位移为Δr i,微小曲线段的长度近似为微小位移Δr i的大小,即Δr i 。每个微小曲线段上的变力近似地用恒力F i代替。这里采用以直线段代替曲线段、以恒力代替变力的方法。则任一曲线段上变力做的功就可以近似地表示为
![]()
那么,变力F在空间中从a到b的曲线段上做的总功可近似为
![]()
当物体所经路线在空间上分割越细,即分割的微小曲线段越多,且每个微小曲线段越小,小到所有微小曲线段长度都趋于0时,上式的极限值即为变力F从a位置到b位置做功的精确值。此方法为定积分计算变力做功的基本思想。
上述思想还可以简化为,沿路径进行无限分割,得到很多元位移d r,如图4.4所示,在每个元位移d r内,可以近似认为F是恒定的。
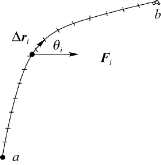
图4.3 变力的功
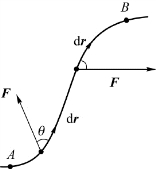
图4.4 元功
在元位移d r内F做的元功为

这一积分在数学上叫作力F沿路径从A到B的线积分。功是一个过程量,本质上是描述力作用于物体的空间积累效应的物理量。(https://www.daowen.com)
不论是恒力还是变力,不论是引力、电磁力、核力还是弹力、张力、摩擦力、理想气体对活塞的压力做功等,各种情况下功的计算都可以用式(4.4)。
若质点做直线运动,受与速度方向成θ的恒力作用,可以得出
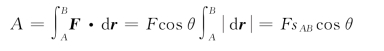
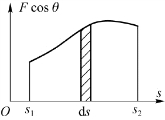
图4.5 变力的功
其中,s AB是质点从A到B经过的位移大小。这即时我们中学所熟知的公式。
根据上述分析可以知道,重力对沿水平方向运动的物体不做功;匀速圆周运动的物体,向心力不做功。
根据积分式的几何意义,可以得到功的几何意义,即功在数值上等于图4.5所示曲线下的面积。
在直角坐标系下,功的计算公式为
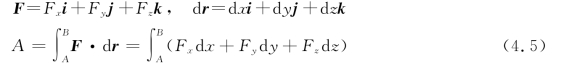
功率定义为单位时间力对物体所做的功。设Δt时间内力F做功ΔA,则平均做功快慢可用平均功率表示,即
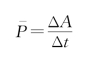
取Δt→0的极限,则瞬时功率的表达式为
![]()
瞬时功率简称功率。功率用以表示力做功的快慢,也可以理解为力做功的速率。功率又可以表示为
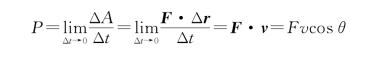
功率为力与质点速度的标积。当力的方向与物体运动的速度方向垂直时,这个力对物体是不做功的。上面的表达式有很重要的实用价值。任何机器往往有其额定的功率,由上式可知,如果要求机器提供的力越大,速度就会越小。汽车在行驶过程中常常需要换挡就是由于这个原因。
在国际单位制中,功率的单位为W(瓦)。
