附录 矢量代数的基本知识
1.标量和矢量的概念
(1)定义
标量只有大小,如质量、长度、时间、密度、能量、温度等。
矢量既有大小又有方向,并有一定的运算规则,如位移、速度、加速度、角速度、力矩、角动量、电场强度、磁感应强度等。
(2)矢量的几种表示方式
·几何表示:有指向的线段;
·解析表示:A=(A 1,A 2,A 3);
![]()
(3)矢量相等
两个矢量大小相等,方向相同。
(4)单位矢量
长度为一个单位的矢量,即e A=A/A。
2.矢量的运算法则
(1)加法(矢量的合成)
含平行四边形法则和三角形法则,如附图1和附图2所示。
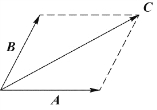
附图1 平行四边形法则
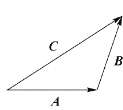
附图2 三角形法则
加法C=A+B满足以下两个性质。
·交换律:A+B=B+A;
·结合律:A+(B+C)=(A+B)+C;
零矢量的定义:A+0=A。
(2)矢量的数乘

结合律:λ(μA)=(λμ)A;
分配律:λ(A+B)=λA+λB。(https://www.daowen.com)
(3)矢量的分解
在一个平面内,若存在两个不共线的矢量e 1和e 2,则平面内的任一矢量可以分解为:A=A 1e 1+A 2e 2。
①正交分解:选择e 1⊥e 2;
②三维空间中应有3个不共面的矢量。
(4)矢量的标积(点积、内积)
①定义S=A·B=AB cosθ,其中θ为A与B的夹角。如果B为单位矢量,则A·B为矢量A在B方向上的投影(分量)。
②性质。
·交换律:A·B=B·A。
·分配律:A·(αB+βC)=αA·B+βA·C。
A·A=A 2≥0。
若A·B=0,则可能是A=0或B=0或A⊥B。
(5)矢量的矢积(叉积、外积)
①定义:A×B=C。
![]()
·方向:A至B右手螺旋方向,如附图3所示。
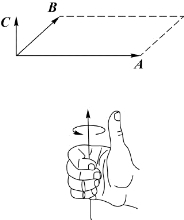
附图3
②性质。
A×B=-B×A
A×(αB+βC)=αA×B+βA×C
A×A=0
A×(B×C)=B(A·C)-C(A·B)
(6)比较。
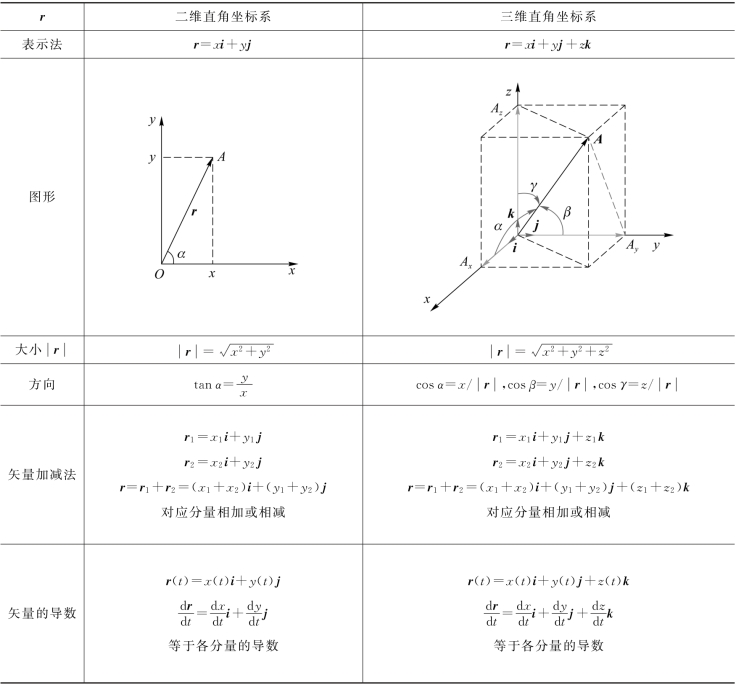
在二维和三维直角坐标系下位置矢量的计算如附表1所示。
附表1 二维与三维直角坐标系下位置矢量的计算