7.3.2 磁通量 磁场的高斯定理
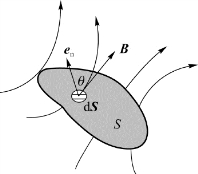
图7.9 磁通量
通过磁场中任一曲面的磁感应线(B线)条数,称为通过该曲面的磁通量,又称B通量,用Φm表示。磁通量是标量,但它有正、负之分。磁通量Φm的计算方法与电通量Φe的计算方法类似。如图7.9所示,在磁场中任一给定曲面S上取面积元d S,若d S的法线e n的方向与该处磁感应强度B的夹角为θ,则通过面积元d S的磁通量为
其中,d S是面积元矢量,其大小等于d S,其方向沿法线e n的方向。
通过整个曲面S的磁通量等于通过此面积上所有面积元磁通量的代数和,即
在国际单位制中,磁通量的单位是韦伯,符号为Wb,1 Wb=1 T·m2。
对闭合曲面来说,规定取垂直于曲面向外的指向为法线e n的正方向。于是磁感应线从闭合曲面穿出时的磁通量为正值(θ＜π/2),磁感应线穿入闭合曲面时的磁通量为负值(θ＞π/2)。由于磁感应线是无头无尾的闭合线,所以穿入闭合曲面的磁感应线数必然等于穿出闭合曲面的磁感应线数。因此,通过磁场中任一闭合曲面的磁通量恒等于零。这一结论称作磁场中的高斯定理,即
式(7.11)与静电场中的高斯定理相对应,但两者有本质上的区别。在静电场中,由于自然界有独立存在的自由电荷,所以通过某一闭合曲面的电通量可以不为零,其中
,说明静电场是有源场。在磁场中,因自然界没有单独存在的磁极,所以通过任一闭合面的磁通量必恒等于零,即
,说明磁场是无源场,或者说是涡旋场。
例7.4 真空中有一无限长直导线CD,通以电流I=10.0 A,一矩形EFGH与CD共面,如图7.10所示,其中a=d=10.0 cm,b=20.0 cm。求通过矩形EFGH面积S的磁通量。
解 由于无限长直线电流在面积S上各点所产生的磁感应强度B的大小随r不同而不同,所以计算通过S面的磁通量B时要用积分。为了便于运算,可将矩形面积S划分成无限多与直导线CD平行的细长条面积元d S=b d r,设其中某一面积元d S与CD相距r,d S上各点B的大小视为相等,B的方向垂直纸面向里。取d S的方向(也就是矩形面积的法线方向)也垂直纸面向里,则
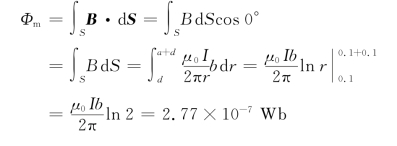
图7.10 例7.4用图