5.3.2 高斯定理的应用
例5.5 如图5.15所示,一均匀带电球面,半径为R,电量为+q,求球面内外任意一点的场强。
解 由题意知,电荷分布是球对称的,产生的电场是球对称的,场强方向沿半径向外,以O为球心,任意球面上的各点E值相等。
(1)球面内任一点P 1的场强
以O为圆心,通过点P 1作半径为r 1的球面S 1为高斯面,高斯定理为
![]()
因为E与d S同向,且S 1上E值不变,所以
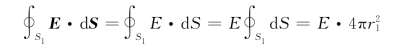
因为
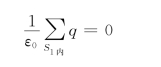
所以
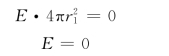
即均匀带电球面内任一点P 1场强为零。
注意:①不是每个面元上的电荷在球面内产生的场强为零,而是所有面元上的电荷在球面内产生场强的矢量和为零。
②非均匀带电球面在球面内任一点产生的场强不可能都为零(在个别点有可能为零)。(2)球面外任一点的场强
以O为圆心,通过点P 2以半径r 2作一球面S 2作为高斯面,由高斯定理有
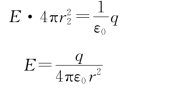
方向:沿半径方向且向外(若q<0,则沿半径方向且向内)。
均匀带电球面外任一点的场强,如同电荷全部集中在球心处的点电荷在该点产生的场强一样,即
E-r曲线如图5.16所示。
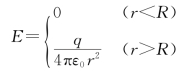
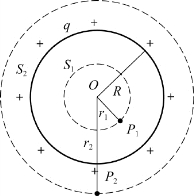
图5.15 例5.5用图(均匀带电球面的场强)
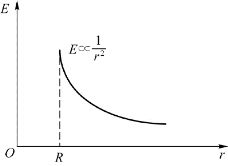
图5.16 例5.5中均匀带电球面的E-r曲线
例5.6 有均匀带电的球体,半径为R,电量为+q,求球内、外的场强。
解 由题意知,电荷分布具有球对称性,所以电场也具有对称性,场强方向由球心向外辐射,在以O为球心的任意球面上各点的E大小相等。
(1)如图5.17所示,以O为球心,过P 1点作半径为r 1的高斯球面S 1,由高斯定理知
![]()
因为E与d S同向,且S 1上各点E大小相等,所以
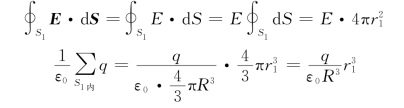
因为
所以
![]()
![]()
E的方向从O指向P 1(若q<0,则E从P 1指向O)。
注意:不要认为S 1外任一电荷元在P 1点处产生的场强为0,而是S 1外所有电荷元在P 1点产生的场强的叠加为0。
(2)球外任意一点P 2。
以O为球心,过P 2点作半径为r 2的球形高斯面S 2,由高斯定理知
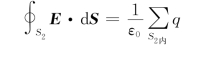
由此有
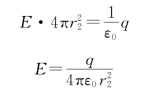
结论:均匀带电球体外任一点的场强,如同电荷全部集中在球心处的点电荷产生的场强一样,即
E-r曲线如图5.18所示。
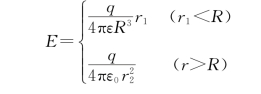
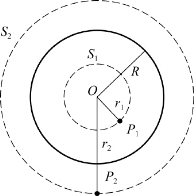
图5.17 例5.6用图(均匀带电球体)
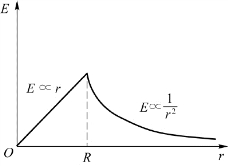
图5.18 例5.6中均匀带电球体的E-r曲线
例5.7 如图5.19所示,一无限长均匀带电直线,设电荷线密度为+λ,求直线外任一点的场强。
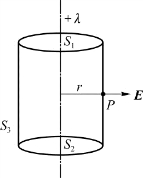
图5.19 例5.17用图(均匀带电直线)
解 由题意知,这里的电场是关于直线轴对称的,E的方向垂直直线。在以直线为轴的任一圆柱面上的各点场强大小是等值的。以直线为轴线,过考察点P作半径为r、高为h的圆柱高斯面,上底为S 1,下底为S 2,侧面为S 3。
由高斯定理得
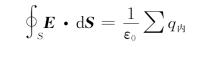
在此,有
![]()
因为在S 1、S 2上各面元d S⊥E,所以前两项积分为0。又因为在S 3上E与d S方向一致,且E=常数,所以
因为(https://www.daowen.com)
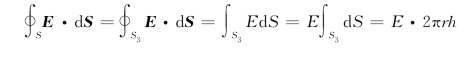
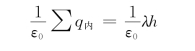
所以
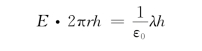
即
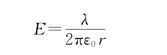
E由带电直线指向考察点(若λ<0,则E由考察点指向带电直线)。
例5.8 图5.20所示的无限长均匀带电圆柱面半径为R,电荷面密度为σ>0,求柱面内、外任一点的场强。
解 由题意知,柱面产生的电场具有轴对称性,场强方向由柱面轴线向外辐射,并且任意以柱面轴线为轴的圆柱面上各点E值相等。
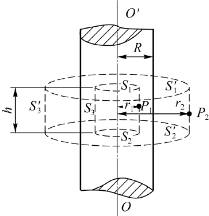
图5.20 例5.8用图(均匀带电圆柱面)
(1)带电圆柱面内任一点P 1的场强。
以OO′为轴,过点P 1作以r 1为半径、高为h的圆柱高斯面,上底为S 1,下底为S 2,侧面为S 3。由高斯定理知
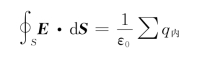
在此,有
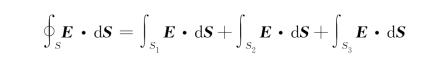
因为在S 1、S 2上各面元d S 1⊥E,所以上式前两项积分为0。又因为在S 3上d S与E同向,且E=常数,所以
因为
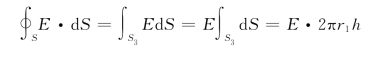
![]()
所以
E·2πr 1h=0
即
E=0
结论:无限长均匀带电圆柱内任一点场强为0。
(2)带电柱面外任一点的场强。
以OO′为轴,过点P 2作半径为r 2、高为h的圆柱形高斯面,上底为S′1,下底为S′2,侧面为S′3。由高斯定理有
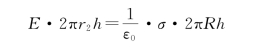
可得
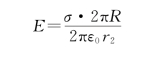
因为
σ·2πR=σ·(2πR·1)=单位长柱面的电荷(电荷线密度)=λ
所以
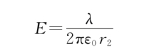
E由轴线指向P 2。当σ<0时,E由P 2指向轴线。
结论:无限长均匀带电圆柱面在其外任一点的场强,与全部电荷都集中在带电柱面的轴线上的无限长均匀带电直线产生的场强一样。
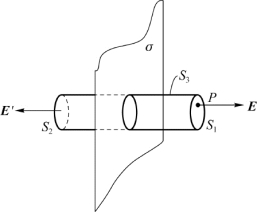
图5.21 例5.9用图(无限大均匀带电平面)
例5.9 如图5.21所示,无限大均匀带电平面电荷面密度为+σ,求平面外任一点的场强。
解 由题意知,平面产生的电场是关于平面两侧对称的,场强方向垂直于平面,与平面距离相等的任意两点处的E值相等。设P为考察点,过点P作一底面平行于平面、关于平面对称的圆柱形高斯面,右端面为S 1,左端面为S 2,侧面为S 3,由高斯定理知
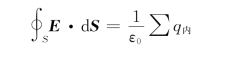
在此,有
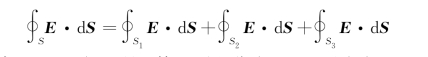
因为在S 3上的各面元d S⊥E,所以第三项积分为0。又因为在S 1、S 2上各面元d S与E同向,且在S 1、S 2上E的大小是常数,所以有
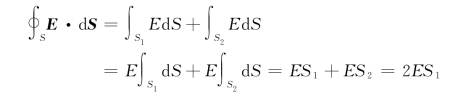
因为
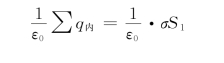
所以
![]()
即

E垂直于平面指向考察点(若σ<0,则E由考察点指向平面)。此结论与例5.4完全一致。
前面我们应用高斯定理求出了几种带电体产生的场强,从这几个例子可以看出,用高斯定理求场强是比较简单的。但是,我们应该明确,虽然高斯定理是普遍成立的,但并不是任何带电体产生的场强都能由它计算出,因为这样的计算是有条件的,它要求电场分布具有一定的对称性,在具有某种对称性时,才能适选高斯面,从而很方便地计算。应用高斯定理时,一般步骤如下:
①分析对称性;
②选择适当的高斯面;
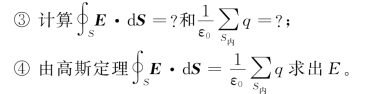
利用高斯定理可以求解具有高度对称性的带电体系所产生的电场的场强。具体的方法是:首先通过对已知电荷分布的对称性分析确定它产生的电场的对称性,然后选取一个恰当的闭合曲面(简称为高斯面),并将高斯定理用于高斯面就可以求出该带电体系所产生的电场的场强。使用这种方法计算场强的关键有两个:一是电荷分布有高度的对称性;二是高斯面的选取要恰当。高斯面选取的技巧是使得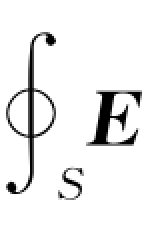 ·d S中的E能以标量的形式从积分号内提出来。一般有三种情况,即球(点)对称、轴对称和面对称。
·d S中的E能以标量的形式从积分号内提出来。一般有三种情况,即球(点)对称、轴对称和面对称。
