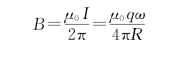7.2* 匀速运动点电荷的磁场
我们知道,电流是一切磁现象的根源,而电流是由于电荷定向运动形成的。可见,电流的磁场本质上是运动电荷产生的。因此,我们可以从电流元所产生的磁场公式推导出运动电荷所产生的磁场公式。
如图7.5所示,有一段粗细均匀的直导线,电流强度为I,横截面面积为S,在其上取一电流元I d l,它在空间某一点P产生的磁感应强度为d B,有
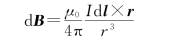
其中,r为电流元到P点的矢径。
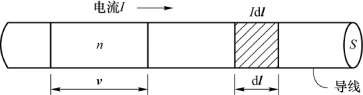
图7.5 电流元与运动电荷
按经典电子理论,金属导体中的电流是大量自由电子的定向运动形成的,为研究方便,我们可等效地认为该电流是正电荷产生的,正电荷的运动方向就是电流的方向。设电荷(正电荷,下同)的电量为q,单位体积内有n个做定向运动的电荷,它们的运动速度均为v。
在导线上取长为v的一柱体,那么在单位时间内通过此柱体右端面S的电荷数为n(vS);单位时间内通过此面的电量为q(nvS)。
由电流强度的定义有
![]()
故
I d l=qnvS d l
因为v与d l同向,所以
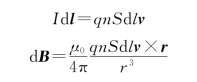
因为该电流元内定向运动的电荷数目为d N=n·(S d l),所以电流元内一个运动电荷产生的磁感应强度为
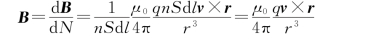 (https://www.daowen.com)
(https://www.daowen.com)
即

其中,r是由运动电荷到考察点的矢量。此式对正、负电荷均成立。
若q>0,B与v同向;若q<0,B与v反向。研究运动电荷的磁场,在理论上就是研究毕奥-萨伐尔定律的微观意义,如图7.6所示。
例7.3 如图7.7所示,设电量为+q的粒子以角速度ω做半径为R的匀速圆周运动,求在圆心处产生的B。
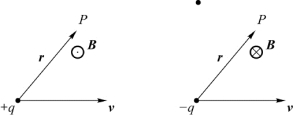
图7.6 运动电荷的磁场
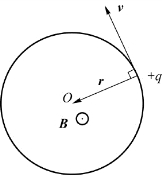
图7.7 例7.3用图(匀速圆周运动的带电粒子的磁场)
解 方法一:由![]() 知,运动电荷产生的B大小为
知,运动电荷产生的B大小为
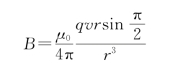
因为r=R,v=Rω,所以![]() ,方向为垂直纸面向外。
,方向为垂直纸面向外。
方法二:利用圆电流产生B的公式,有电荷运动,则形成电流。在此,+q形成的电流与+q运动的轨迹(圆周)重合,且电流为逆时针方向,相当于一个平面圆形载流线圈。可知,B的方向垂直纸面向外。根据平面圆形载流线圈在其中心产生B的公式,可求出B的大小。
设运动频率为f,可有
![]()
可知