8.4.1 自感
当一个电流回路的电流i随时间变化时,通过回路自身的全磁通也发生变化,因而回路自身也产生感生电动势(图8.12)。这就是自感现象,产生的感生电动势叫作自感电动势。在这里,全磁通与回路中的电流成正比,即其中,比例系数L叫作回路的自感系数(简称自感),它取决于回路的大小、形状、线圈的匝数以及它周围的磁介质的分布。在国际单位制中,自感系数的单位名称是亨,符号为H。
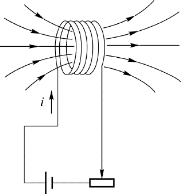
图8.12 自感现象
由电磁感应定律,在L一定的条件下自感电动势为
在图8.12中,回路的正方向一般取电流i的方向。当电流增大,即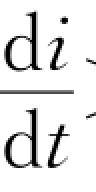
＞0时,由式(8.20)知εL＜0,说明εL的方向与电流的方向相反;当
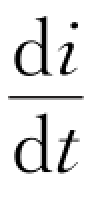＜0时,由式(8.20)知εL＞0,说明εL的方向与电流的方向相同。由此可知,自感电动势的方向总是要使它阻碍回路本身电流的变化。
例8.5 计算一个螺绕环的自感。设环的截面积为S,轴线半径为R,单位长度上的匝数为n,环中充满相对磁导率为μr的磁介质。
解 设螺绕环绕组通有电流为i,由于螺绕环管内磁场B=μ0μr ni,所以管内全磁通为
Ψ=NΦ=2πRn·BS=2πμ0μr Rn 2Si
由自感定义式,得此螺绕环的自感为
由于2πRS=V为螺绕环管内的体积,所以螺绕环自感又可写成
此结果表明,环内充满磁介质时,其自感系数比在真空时要增大到μr倍。
例8.6 一根电缆由同轴的两个薄壁金属管构成,半径分别为R 1和R 2,两管壁间充以μr=1的电介质。电流由内管流走,由外管流回。试求单位长度的这种电缆的自感系数。
解 这种电缆可视为单匝回路(图8.13),其磁通量即通过任一纵截面的磁通量。以I表示通过的电流,则在两管壁间距轴r处的磁感应强度为
而通过单位长度纵截面的磁通量为
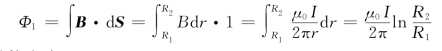
单位长度的自感系数应为
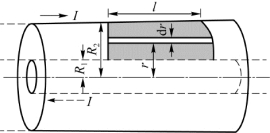
图8.13 例8.6用图(电缆的磁通量计算)
例8.7 RL电路。如图8.14(a)所示,由一自感线圈L、电阻R与电源ε组成的电路。当开关K与端a相接触时,自感线圈和电阻串联而与电源相接,求接通后电流的变化情况。待电流稳定后,再迅速将开关打向b端,求此后的电流变化情况。
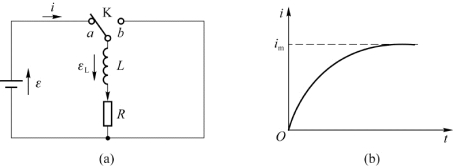
图8.14 例8.7用图一(RL电路)
解 从开关K接通电源开始,电流是变化的。由于电流变化比较慢,所以在任一时刻基尔霍夫第二方程仍然成立。对于整个电路,在图8.14(a)所示电流与电动势方向的情况下,基尔霍夫第二方程为
式(8.23)的指数L/R具有时间的量纲,称为此电路的时间常数。常以τ表示时间常数,即τ=L/R。开关接通后经过时间τ,电流与其最大值的差为最大值的1/e。当t大于τ的若干倍之后,电流基本上达到最大值,就可以认为是稳定的了。图8.14(b)给出了上述电路中电流随时间增长的情况。
当开关K由a换到b后(图8.15(a)),对整个回路,基尔霍夫第二方程为
这一结果说明,电流随时间按指数规律减小。当t=τ时,i减小为原来的1/e。式(8.24)所示的电流与时间的关系曲线如图8.15(b)所示。
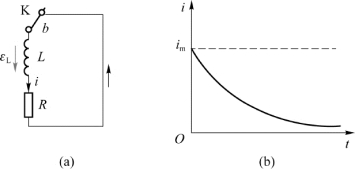
图8.15 例8.7用图二
式(8.23)和式(8.24)所表示的电流变化情况还可以用实验演示。在图8.16(a)所示的实验中,当合上开关后,A灯比B灯先亮,就是因为在合上开关后,A、B两支路同时接通,但B灯的支路中有一多匝线圈,自感系数较大,因而电流增长较慢。而在图8.16(b)所示的实验中,在打开开关时,灯泡突然强烈地闪亮一下再熄灭,就是因为多匝线圈支路中较大的电流在开关打开后通过灯泡而又逐渐消失的缘故。
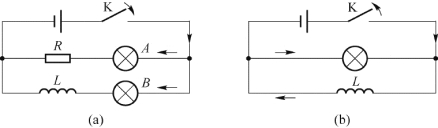
图8.16 自感现象演示